AMC 10 2022 Test A
Instructions
- This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.
- You will receive 6 points for each correct answer, 2.5 points for each problem left unanswered if the year is before 2006, 1.5 points for each problem left unanswered if the year is after 2006, and 0 points for each incorrect answer.
- No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers (and calculators that are accepted for use on the test if before 2006. No problems on the test will require the use of a calculator).
- Figures are not necessarily drawn to scale.
- You will have 75 minutes working time to complete the test.
What is the value of\[3+\frac{1}{3+\frac{1}{3+\frac13}}?\]$\textbf{(A)}\ \dfrac{31}{10}\qquad\textbf{(B)}\ \dfrac{49}{15}\qquad\textbf{(C)}\ \dfrac{33}{10}\qquad\textbf{(D)}\ \dfrac{109}{33}\qquad\textbf{(E)}\ \dfrac{15}{4}$
$\textbf{D}$
\begin{align*}
3+\frac{1}{3+\frac{1}{3+\frac13}} &= 3+\frac{1}{3+\frac{1}{\frac{10}{3}}} \\
&= 3+\frac{1}{3+\frac{3}{10}} \\
&= 3+\frac{1}{\frac{33}{10}} \\
&= 3+\frac{10}{33} \\
&=\frac{109}{33}
\end{align*}
Mike cycled $15$ laps in $57$ minutes. Assume he cycled at a constant speed throughout. Approximately how many laps did he complete in the first $27$ minutes?
$\textbf{(A) } 5 \qquad\textbf{(B) } 7 \qquad\textbf{(C) } 9 \qquad\textbf{(D) } 11 \qquad\textbf{(E) } 13$
$\textbf{B}$
It takes him $\dfrac{57}{15}=\dfrac{19}{5}$ minutes to complete 1 lap. So in the first 27 minutes he completed $27\div\dfrac{19}{5}=\dfrac{135}{19}\approx7$ laps.
The sum of three numbers is $96.$ The first number is $6$ times the third number, and the third number is $40$ less than the second number. What is the absolute value of the difference between the first and second numbers?
$\textbf{(A) } 1 \qquad \textbf{(B) } 2 \qquad \textbf{(C) } 3 \qquad \textbf{(D) } 4 \qquad \textbf{(E) } 5$
$\textbf{E}$
Let $x$ be the third number. It follows that the first number is $6x,$ and the second number is $x+40.$ We have \[6x+(x+40)+x=8x+40=96\] from which $x=7.$
Therefore, the first number is $42,$ and the second number is $47.$ The absolute value of the difference is $|42-47|=5$.
In some countries, automobile fuel efficiency is measured in liters per $100$ kilometers while other countries use miles per gallon. Suppose that 1 kilometer equals $m$ miles, and $1$ gallon equals $l$ liters. Which of the following gives the fuel efficiency in liters per $100$ kilometers for a car that gets $x$ miles per gallon?
$\textbf{(A) } \dfrac{x}{100lm} \qquad \textbf{(B) } \dfrac{xlm}{100} \qquad \textbf{(C) } \dfrac{lm}{100x} \qquad \textbf{(D) } \dfrac{100}{xlm} \qquad \textbf{(E) } \dfrac{100lm}{x}$
$\textbf{E}$
The formula for fuel efficiency is\[\frac{\text{Distance}}{\text{Gas Consumption}}\]Note that $1$ mile equals $\dfrac1m$ kilometers, and 1 gallon equals $l$ liters, we have\[\frac{x\text{ miles}}{1\text{ gallon}} = \frac{x\cdot\frac{1}{m}\text{ kilometers}}{l\text{ liters}} = \frac{1\text{ kilometer}}{\frac{lm}{x}\text{ liters}} = \frac{100\text{ kilometers}}{\frac{100lm}{x}\text{ liters}}\]Therefore, the answer is $\dfrac{100lm}{x}.$
Square $ABCD$ has side length $1$. Points $P$, $Q$, $R$, and $S$ each lie on a side of $ABCD$ such that $APQCRS$ is an equilateral convex hexagon with side length $s$. What is $s$?
$\textbf{(A) } \dfrac{\sqrt{2}}{3} \qquad \textbf{(B) } \dfrac{1}{2} \qquad \textbf{(C) } 2 - \sqrt{2} \qquad \textbf{(D) } 1 - \dfrac{\sqrt{2}}{4} \qquad \textbf{(E) } \dfrac{2}{3}$
$\textbf{C}$
In isosceles right triangle $BPQ$ we have $BP=BQ=1-s$, $PQ=s$. So $s=\sqrt2(1-s)$, from which $s=\dfrac{\sqrt2}{1+\sqrt2}=\dfrac{\sqrt2}{1+\sqrt2}\times\dfrac{\sqrt2-1}{\sqrt2-1}=2-\sqrt2$.
Which expression is equal to\[\left|a-2-\sqrt{(a-1)^2}\right|\]for $a<0?$
$\textbf{(A) } 3-2a \qquad \textbf{(B) } 1-a \qquad \textbf{(C) } 1 \qquad \textbf{(D) } a+1 \qquad \textbf{(E) } 3$
$\textbf{A}$
If $a<0$, then we have $a-1<0$. So $\sqrt{(a-1)^2}=1-a$. Hence, we get \begin{align*}
\left|a-2-\sqrt{(a-1)^2}\right| &=\left|a-2-(1-a)\right| \\
&=\left|2a-3\right| \\
&=3-2a
\end{align*}
The least common multiple of a positive integer $n$ and $18$ is $180$, and the greatest common divisor of $n$ and $45$ is $15$. What is the sum of the digits of $n$?
$\textbf{(A) } 3 \qquad \textbf{(B) } 6 \qquad \textbf{(C) } 8 \qquad \textbf{(D) } 9 \qquad \textbf{(E) } 12$
$\textbf{B}$
Note that \begin{align*}
18 &= 2\times3^2\\
180 &= 2^2\times3^2\times5\\
45 &= 3^2\times5 \\
15 &= 3\times5
\end{align*} Let $n = 2^a\times3^b\times5^c.$
From the least common multiple condition, we have\[\operatorname{lcm}(n,18) = \operatorname{lcm}(2^a\times3^b\times5^c,2\times3^2) = 2^{\max(a,1)}\times3^{\max(b,2)}\times5^{\max(c,0)} = 2^2\times3^2\times5\]from which $a=2, b\in\{0,1,2\},$ and $c=1.$
From the greatest common divisor condition, we have\[\gcd(n,45) = \gcd(2^2\times3^b\times5,3^2\times5) = 2^{\min(2,0)}\times3^{\min(b,2)}\times5^{\min(1,1)} = 3\times5\]from which $b=1.$
Together, we conclude that $n=2^2\times3\times5=60.$ The sum of its digits is $6+0=6.$
A data set consists of $6$ (not distinct) positive integers: $1$, $7$, $5$, $2$, $5$, and $X$. The average (arithmetic mean) of the $6$ numbers equals a value in the data set. What is the sum of all possible values of $X$?
$\textbf{(A) } 10 \qquad \textbf{(B) } 26 \qquad \textbf{(C) } 32 \qquad \textbf{(D) } 36 \qquad \textbf{(E) } 40$
$\textbf{D}$
The average of the 6 numbers is $\dfrac{1+7+5+2+5+X}{6}=\dfrac{X+20}{6}$. The average could be equal to 1, 2, 5, 7 or $X$. Hence, we get 5 equations $$\dfrac{X+20}{6}=1, 2, 5, 7 \text{ or } X$$ Solving, we get $X=-14, -8, 10, 22 \text{ or } 4$. Since $X$ is a positive integer, only 10, 22 and 4 are possible values of $X$. The answer is $10+22+4=36$.
A rectangle is partitioned into $5$ regions as shown. Each region is to be painted a solid color - red, orange, yellow, blue, or green - so that regions that touch are painted different colors, and colors can be used more than once. How many different colorings are possible?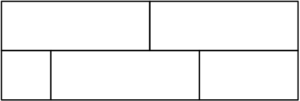
$\textbf{(A) }120\qquad\textbf{(B) }270\qquad\textbf{(C) }360\qquad\textbf{(D) }540\qquad\textbf{(E) }720$
$\textbf{D}$
The top-left region has 5 coloring choices. Then the top-right region has 4 coloring choices, and the middle region in the bottom row has 3 coloring choices. Now both the bottom-left and bottom-right regions each have 3 coloring choices. Therefore, the total number of coloring arrangements is $5\times4\times3\times3\times3=540$.
Daniel finds a rectangular index card and measures its diagonal to be $8$ centimeters. Daniel then cuts out equal squares of side $1$ cm at two opposite corners of the index card and measures the distance between the two closest vertices of these squares to be $4\sqrt{2}$ centimeters, as shown below. What is the area of the original index card?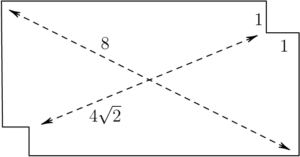
$\textbf{(A) } 14 \qquad \textbf{(B) } 10\sqrt{2} \qquad \textbf{(C) } 16 \qquad \textbf{(D) } 12\sqrt{2} \qquad \textbf{(E) } 18$
$\textbf{E}$
Let the length and width of the original index card be $x$ and $y$, respectively. The area of the original index card is $xy$. We can set up equations based on the lengths of the diagonals:
\begin{align*}
x^2+y^2&=8^2\\
(x-2)^2+(y-2)^2&=\left(4\sqrt2\right)^2
\end{align*} From the second equation we get $x^2+y^2-4x-4y=24$. Subtracting the first equation, we have $4x+4y=40$, or $x+y=10$. Since we want to find the value of $xy$, we square the equation to get $x^2+2xy+y^2=100$. Then subtracting the first equation again, we get $2xy=36$. The answer is $xy=18$.
Ted mistakenly wrote $2^m\cdot\sqrt{\dfrac{1}{4096}}$ as $2\cdot\sqrt[m]{\dfrac{1}{4096}}.$ What is the sum of all real numbers $m$ for which these two expressions have the same value?
$\textbf{(A) } 5 \qquad \textbf{(B) } 6 \qquad \textbf{(C) } 7 \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9$
$\textbf{C}$
We see that $\dfrac{1}{4096}=2^{-12}$. So \begin{align*}
2^m\cdot\sqrt{\dfrac{1}{4096}}&=2^m\cdot2^{-6}=2^{m-6}\\ 2\cdot\sqrt[m]{\dfrac{1}{4096}}&=2\cdot2^{-\dfrac{12}{m}}=2^{1-\dfrac{12}{m}}
\end{align*} Hence, we get $2^{m-6}=2^{1-\dfrac{12}{m}}$, from which $m-6=1-\dfrac{12}{m}$. Solving, we get $m=3 \text{ or } 4$. The sum of all possible values of $m$ is $3+4=7$.
On Halloween $31$ children walked into the principal's office asking for candy. They can be classified into three types: Some always lie; some always tell the truth; and some alternately lie and tell the truth. The alternaters arbitrarily choose their first response, either a lie or the truth, but each subsequent statement has the opposite truth value from its predecessor. The principal asked everyone the same three questions in this order.
“Are you a truth-teller?” The principal gave a piece of candy to each of the $22$ children who answered yes.
“Are you an alternater?” The principal gave a piece of candy to each of the $15$ children who answered yes.
“Are you a liar?” The principal gave a piece of candy to each of the $9$ children who answered yes.
How many pieces of candy in all did the principal give to the children who always tell the truth?
$\textbf{(A) } 7 \qquad \textbf{(B) } 12 \qquad \textbf{(C) } 21 \qquad \textbf{(D) } 27 \qquad \textbf{(E) } 31$
$\textbf{A}$
Note that:
$\bullet$ Truth-tellers would answer yes-no-no to the three questions in this order.$\newline$
$\bullet$ Liars would answer yes-yes-no to the three questions in this order.$\newline$
$\bullet$ Alternaters who responded truth-lie-truth would answer no-no-no to the three questions in this order.$\newline$
$\bullet$ Alternaters who responded lie-truth-lie would answer yes-yes-yes to the three questions in this order.
Suppose that there are $T$ truth-tellers, $L$ liars, and $A$ alternaters who responded lie-truth-lie.
The conditions of the first two questions imply that \begin{align*}
T+L+A&=22\\
L+A&=15
\end{align*} Subtracting the second equation from the first, we have $T=22-15=7$. Since the truth-tellers answer yes to the first question only, they get 7 pieces of candy in total.
The condition of the third question is superfluous for this question.
Let $\triangle ABC$ be a scalene triangle. Point $P$ lies on $\overline{BC}$ so that $\overline{AP}$ bisects $\angle BAC.$ The line through $B$ perpendicular to $\overline{AP}$ intersects the line through $A$ parallel to $\overline{BC}$ at point $D.$ Suppose $BP=2$ and $PC=3.$ What is $AD?$
$\textbf{(A) } 8 \qquad \textbf{(B) } 9 \qquad \textbf{(C) } 10 \qquad \textbf{(D) } 11 \qquad \textbf{(E) } 12$
$\textbf{C}$
Suppose that $\overline{BD}$ intersects $\overline{AP}$ and $\overline{AC}$ at $X$ and $Y,$ respectively. We see that $\triangle ABX\cong\triangle AYX.$ So $AB=AY$.
Since $AP$ bisects $\angle BAC$, the distance from $P$ to $\overline{AB}$ is the same as the distance from $P$ to $\overline{AC}$. Hence, the ratio of the area of $\triangle ABP$ to the area of $\triangle ACP$ is $\dfrac{AB}{AC}$. However, the ratio of the area of $\triangle ABP$ to the area of $\triangle ACP$ can also be defined as $\dfrac{BP}{CP}=\dfrac23$. Therefore, we get $\dfrac{AB}{AC}=\dfrac23$. Since $AB=AY$, we have $\dfrac{AY}{AC}=\dfrac23$, from which $\dfrac{AY}{YC}=2$.
Given that $AD\parallel BC$, we get $\triangle ADY \sim \triangle CBY$. So $\dfrac{AD}{CB}=\dfrac{AY}{CY}=2$. It follows that $AD=2BC=2(BP+PC)=10.$
How many ways are there to split the integers $1$ through $14$ into $7$ pairs such that in each pair, the greater number is at least $2$ times the lesser number?
$\textbf{(A) } 108 \qquad \textbf{(B) } 120 \qquad \textbf{(C) } 126 \qquad \textbf{(D) } 132 \qquad \textbf{(E) } 144$
$\textbf{E}$
Clearly, the integers from $8$ through $14$ must be in different pairs, so are the integers from $1$ through $7.$
$7$ must pair with $14.$$\newline$
When the position of 7 is confirmed, $6$ can pair with either $12$ or $13.$$\newline$
When the position of 6 is confirmed, $5$ can pair with any of the three remaining numbers from $10,11,12,13.$$\newline$
Finaly, $1,2,3,4$ can pair with the other four remaining numbers from $8,9,10,11,12,13$ without restrictions.
Hence, the total number of arrangements is $1\times2\times3\times4!=144$.
Quadrilateral $ABCD$ with side lengths $AB=7, BC=24, CD=20, DA=15$ is inscribed in a circle. The area interior to the circle but exterior to the quadrilateral can be written in the form $\dfrac{a\pi-b}{c},$ where $a,b,$ and $c$ are positive integers such that $a$ and $c$ have no common prime factor. What is $a+b+c?$
$\textbf{(A) } 260 \qquad \textbf{(B) } 855 \qquad \textbf{(C) } 1235 \qquad \textbf{(D) } 1565 \qquad \textbf{(E) } 1997$
$\textbf{D}$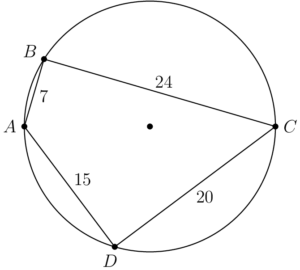
By observation, we see that $7^2+24^2=15^2+20^2=25^2$. So we guess $\angle B=\angle D=90^\circ$, which means $AC$ is the diameter of the circle. Now we need to prove it.
In $\triangle ABC$ we have $$AC^2=AB^2+BC^2-2AB\times BC\cos\angle B=7^2+24^2-2\times7\times24\cos\angle B$$ In $\triangle ACD$ we have $$AC^2=AD^2+CD^2-2AD\times CD\cos\angle D=15^2+20^2-2\times15\times20\cos\angle D$$ Hence, we get $$7^2+24^2-2\times7\times24\cos\angle B=15^2+20^2-2\times15\times20\cos\angle D$$ Since $7^2+24^2=15^2+20^2=25^2$, we get $$7\times24\cos\angle B=15\times20\cos\angle D$$ Opposite angles of cyclic quadrilateral are supplementary, so\[\angle B + \angle D = 180^{\circ}\] Therefore, we get $\angle B=\angle D=90^\circ$, $\cos\angle B=\cos\angle D=0$. The diameter of the circle is $AC=25$.
The area of $\triangle ABC$ is $\dfrac12\times7\times24=84$. The area of $\triangle ACD$ is $\dfrac12\times15\times20=150$. The area of the circle is $\pi\left(\dfrac{25}2\right)^2=\dfrac{625\pi}{4}$. So the area interior to the circle but exterior to the quadrilateral is $$\dfrac{625\pi}{4}-84-150=\dfrac{625\pi-936}{4}=\dfrac{a\pi-b}{c}$$ Hence, we get $a=625$, $b=936$, $c=4$. The answer is $625+936+4=1565$.
The roots of the polynomial $10x^3 - 39x^2 + 29x - 6$ are the height, length, and width of a rectangular box (right rectangular prism). A new rectangular box is formed by lengthening each edge of the original box by $2$ units. What is the volume of the new box?
$\textbf{(A) } \dfrac{24}{5} \qquad \textbf{(B) } \dfrac{42}{5} \qquad \textbf{(C) } \dfrac{81}{5} \qquad \textbf{(D) } 30 \qquad \textbf{(E) } 48$
$\textbf{D}$
Let $a,b,c$ be the roots of the polynomial. By Vieta's formulas, we have \begin{align*}
a+b+c&=\dfrac{39}{10}\\
ab+ac+bc&=\dfrac{29}{10}\\
abc&=\dfrac{6}{10}
\end{align*} The volume of the new box is $$(a+2)(b+2)(c+2)=abc+2(ab+ac+bc)+4(a+b+c)+8=30$$
How many three-digit positive integers $\underline{a} \ \underline{b} \ \underline{c}$ are there whose nonzero digits $a,b,$ and $c$ satisfy\[0.\overline{\underline{a}~\underline{b}~\underline{c}} = \frac{1}{3} (0.\overline{a} + 0.\overline{b} + 0.\overline{c})?\](The bar indicates repetition, thus $0.\overline{\underline{a}~\underline{b}~\underline{c}}$ is the infinite repeating decimal $0.\underline{a}~\underline{b}~\underline{c}~\underline{a}~\underline{b}~\underline{c}~\cdots$)
$\textbf{(A) } 9 \qquad \textbf{(B) } 10 \qquad \textbf{(C) } 11 \qquad \textbf{(D) } 13 \qquad \textbf{(E) } 14$
$\textbf{D}$
Note that $0.\overline{a}=\dfrac{a}9$, and $0.\overline{\underline{a}~\underline{b}~\underline{c}} =\dfrac{\underline{a} \ \underline{b} \ \underline{c}}{999}$, we have $$\frac{100a+10b+c}{999} = \frac13\left(\frac a9 + \frac b9 + \frac c9\right) $$ which can be simplified as $$7a=3b+4c$$ Hence, we get \begin{align*}
0&\equiv 3b-3c\pmod{7} \\
b&\equiv c\pmod{7}
\end{align*} So either $b=c$ or $|b-c|=7$.
If $b=c$, we have 9 ordered triples $(a,b,c)=(1,1,1),(2,2,2),\cdots,(9,9,9)$.
If $|b-c|=7$, we have 4 order triples $(a,b,c)=(4,8,1),(5,1,8),(5,9,2),(6,2,9).$
Together, we have $9+4=13$ three-digit positive integers $\underline{a} \ \underline{b} \ \underline{c}$.
Let $T_k$ be the transformation of the coordinate plane that first rotates the plane $k$ degrees counterclockwise around the origin and then reflects the plane across the $y$-axis. What is the least positive integer $n$ such that performing the sequence of transformations $T_1, T_2, T_3,...,T_n$ returns the point $(1, 0)$ back to itself?
$\textbf{(A) } 359 \qquad \textbf{(B) } 360 \qquad \textbf{(C) } 719 \qquad \textbf{(D) } 720 \qquad \textbf{(E) } 721$
$\textbf{A}$
Let $P=(r,\theta)$ be a point in polar coordinates, where $\theta$ is in degrees.
Rotating $P$ by $k^{\circ}$ counterclockwise around the origin gives the transformation $(r,\theta)\rightarrow(r,\theta+k^{\circ}).$ Reflecting $P$ across the $y$-axis gives the transformation $(r,\theta)\rightarrow(r,180^{\circ}-\theta).$ Note that\begin{align*} T_k(P)&=(r,180^{\circ}-\theta-k^{\circ}) \\ T_{k+1}(T_k(P)) &= (r,\theta -1^{\circ}) \end{align*}We start with $(1,0^{\circ})$ in polar coordinates. For the sequence of transformations $T_1, T_2, T_3, \cdots, T_k,$ it follows that
After $T_1,$ we have $(1,179^{\circ}).$$\newline$
After $T_2,$ we have $(1,-1^{\circ}).$$\newline$
After $T_3,$ we have $(1,178^{\circ}).$$\newline$
After $T_4,$ we have $(1,-2^{\circ}).$$\newline$
After $T_5,$ we have $(1,177^{\circ}).$$\newline$
After $T_6,$ we have $(1,-3^{\circ}).$$\newline$
$\cdots\newline$
After $T_{2k-1},$ we have $(1,180^{\circ}-k^{\circ}).$$\newline$
After $T_{2k},$ we have $(1,-k^{\circ}).$
The least such positive integer $k$ is $180.$ Therefore, the least such positive integer $n$ is $2k-1= 359.$
Define $L_n$ as the least common multiple of all the integers from $1$ to $n$ inclusive. There is a unique integer $h$ such that\[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{17}=\frac{h}{L_{17}}\]What is the remainder when $h$ is divided by $17$?
$\textbf{(A) } 1 \qquad \textbf{(B) } 3 \qquad \textbf{(C) } 5 \qquad \textbf{(D) } 7 \qquad \textbf{(E) } 9$
$\textbf{C}$
Notice that $L_{17}$ contains the highest power of every prime below $17$. Thus, we have $$L_{17}=16\times 9 \times 5 \times 7 \times 11 \times 13 \times 17$$ The unique integer $h$ satisfies $$h\equiv\dfrac{L_{17}}1+\dfrac{L_{17}}2+\cdots+\dfrac{L_{17}}{17}\pmod{17}$$ Among all terms on the right side of the equation, $\dfrac{L_{17}}{17}$ is the only term which is not a multiple of 17. Hence, we have \begin{align*}
h&\equiv\dfrac{L_{17}}{17}\pmod{17}\\
&\equiv16\times 9 \times 5 \times 7 \times 11 \times 13\pmod{17}\\
&\equiv(-1)\times 9 \times 5 \times 7 \times 11 \times(-4)\pmod{17}\\
&\equiv4\times9 \times 5 \times 7 \times 11\pmod{17}\\
&\equiv36\times35\times11\pmod{17}\\
&\equiv2\times1\times11\pmod{17}\\
&\equiv5
\end{align*} Therefore, the reminder when $h$ is divided by 17 is 5.
A four-term sequence is formed by adding each term of a four-term arithmetic sequence of positive integers to the corresponding term of a four-term geometric sequence of positive integers. The first three terms of the resulting four-term sequence are $57$, $60$, and $91$. What is the fourth term of this sequence?
$\textbf{(A) } 190 \qquad \textbf{(B) } 194 \qquad \textbf{(C) } 198 \qquad \textbf{(D) } 202 \qquad \textbf{(E) } 206$
$\textbf{E}$
Let the arithmetic sequence be $a,a+d,a+2d,a+3d$ and the geometric sequence be $b,br,br^2,br^3$.
We are given that \begin{align*} a+b&=57 \\ a+d+br&=60 \\ a+2d+br^2&=91 \end{align*} and we want to find $a+3d+br^3.$
Subtracting the first equation from the second and the second equation from the third, we get \begin{align*} d+b(r-1)&=3 \\ d+br(r-1)&=31 \end{align*} Subtract these results, we get\[b(r-1)^2=28\] Assuming that $r$ is an integer. Note that either $(r-1)^2=1$ or $(r-1)^2=4.$ We proceed with casework:
If $(r-1)^2=1,$ then $r=2,b=28,a=29,$ and $d=-25.$ The arithmetic sequence is $29,4,-21,-46,$ arriving at a contradiction.$\newline$
If $(r-1)^2=4,$ then $r=3,b=7,a=50,$ and $d=-11.$ The arithmetic sequence is $50,39,28,17,$ and the geometric sequence is $7,21,63,189.$ This case is valid.
Therefore, The answer is $a+3d+br^3=206.$
A bowl is formed by attaching four regular hexagons of side $1$ to a square of side $1$. The edges of the adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?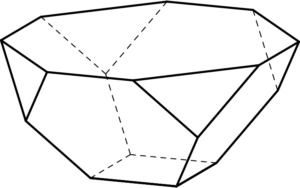
$\textbf{(A) } 6 \qquad \textbf{(B) } 7 \qquad \textbf{(C) } 5+2\sqrt{2} \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9$
$\textbf{B}$
We extend line segments $\ell,m,$ and $n$ to their point of concurrency, as shown below: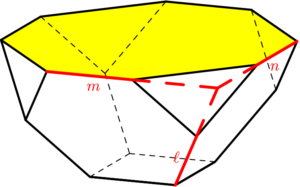
We claim that lines $\ell,m,$ and $n$ are concurrent: In the lateral faces of the bowl, we know that lines $\ell$ and $m$ must intersect, and lines $\ell$ and $n$ must intersect. In addition, line $\ell$ intersects the top plane of the bowl at exactly one point. Since lines $m$ and $n$ are both in the top plane of the bowl, we conclude that lines $\ell,m,$ and $n$ are concurrent.
In the lateral faces of the bowl, the dashed red line segments create equilateral triangles. So the dashed red line segments all have length $1.$ In the top plane of the bowl, we know that $\overleftrightarrow{m}\perp\overleftrightarrow{n}.$ So the dashed red line segments create an isosceles right triangle with leg-length $1.$
Note that octagon in the top plane has four pairs of parallel sides, and the successive side-lengths are $1$,$\sqrt2$,$1$,$\sqrt2$,$1$,$\sqrt2$,$1$,$\sqrt2,$ as shown below: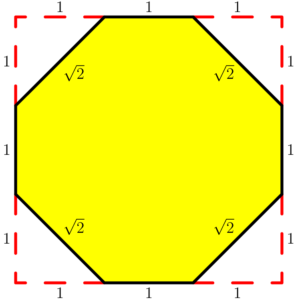
The area of the octagon is\[3^2-4\times\frac12\times1^2=7\]
Suppose that $13$ cards numbered $1, 2, 3, \ldots, 13$ are arranged in a row. The task is to pick them up in numerically increasing order, working repeatedly from left to right. In the example below, cards $1, 2, 3$ are picked up on the first pass, $4$ and $5$ on the second pass, $6$ on the third pass, $7, 8, 9, 10$ on the fourth pass, and $11, 12, 13$ on the fifth pass. For how many of the $13!$ possible orderings of the cards will the $13$ cards be picked up in exactly two passes?![]()
$\textbf{(A) } 4082 \qquad \textbf{(B) } 4095 \qquad \textbf{(C) } 4096 \qquad \textbf{(D) } 8178 \qquad \textbf{(E) } 8191$
$\textbf{D}$
Since the $13$ cards are picked up in two passes, the first pass must pick up the first $n$ cards and the second pass must pick up the remaining cards $n+1$ through $13$. Also note that if $n+1$ is placed before $n$, then $n+1$ will not be picked up on the first pass since cards are picked up in order. Therefore, we want $n+1$ to be placed before $n$ to create a second pass, and that after the first pass, the numbers $n+1$ through $13$ are lined up in order from least to greatest.
To construct this, $n$ cannot be placed in the $n$th position because all cards $1$ to $n-1$ will have to precede it and there will be no room for $n+1$. Therefore, we have $\dbinom{13}{n}-1$ ways to arrange cards $1$ to $n$. Once the positions of the first $n$ cards are confirmed, there is only one way to arrange the rest cards.
Hence, the total number of arrangements is\[\sum_{n=1}^{12}\left[\binom{13}{n}-1\right] = \left[\sum_{n=1}^{12}\binom{13}{n}\right]-12 = \left[\sum_{n=0}^{13}\binom{13}{n}\right]-14 = 2^{13} - 14 = 8178\]
Isosceles trapezoid $ABCD$ has parallel sides $\overline{AD}$ and $\overline{BC},$ with $BC < AD$ and $AB = CD.$ There is a point $P$ in the plane such that $PA=1, PB=2, PC=3,$ and $PD=4.$ What is $\dfrac{BC}{AD}?$
$\textbf{(A) }\dfrac{1}{4}\qquad\textbf{(B) }\dfrac{1}{3}\qquad\textbf{(C) }\dfrac{1}{2}\qquad\textbf{(D) }\dfrac{2}{3}\qquad\textbf{(E) }\dfrac{3}{4}$
$\textbf{B}$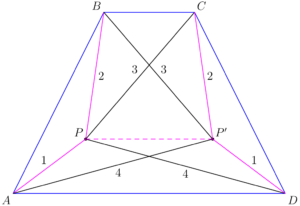
Consider the reflection $P^{\prime}$ of $P$ over the perpendicular bisector of $\overline{BC}$, creating two new isosceles trapezoids $DAPP^{\prime}$ and $CBPP^{\prime}$. Under this reflection, $P^{\prime}D=PA=1$, $P^{\prime}C=PB=2$, $P^{\prime}B=PC=3$, and $P^{\prime}A=PD=4$.
Since $DAPP'$ and $CBPP'$ are isosceles trapezoids, they are cyclic. Using Ptolemy's theorem on $DAPP'$, we get that $PP'\cdot AD + PA\cdot P'D= AP'\cdot PD$, so\[PP' \cdot AD + 1 \times 1 = 4 \times 4\]Then, using Ptolemy's theorem again on $CBPP'$, we get that $BC\cdot PP' + BP\cdot CP' = BP'\cdot CP$, so\[PP' \cdot BC + 2 \times 2 = 3 \times 3\]Thus, we get $PP^{\prime}\cdot AD=15$ and $PP^{\prime}\cdot BC=5$. Dividing these two equations yields $\dfrac{BC}{AD}= \dfrac{1}{3}$.
How many strings of length $5$ formed from the digits $0$, $1$, $2$, $3$, $4$ are there such that for each $j \in \{1,2,3,4\}$, at least $j$ of the digits are less than $j$? (For example, $02214$ satisfies this condition because it contains at least $1$ digit less than $1$, at least $2$ digits less than $2$, at least $3$ digits less than $3$, and at least $4$ digits less than $4$. The string $23404$ does not satisfy the condition because it does not contain at least $2$ digits less than $2$.)
$\textbf{(A) }500\qquad\textbf{(B) }625\qquad\textbf{(C) }1089\qquad\textbf{(D) }1199\qquad\textbf{(E) }1296$
$\textbf{E}$
Let's call the condition where you require at least $j$ digits less than $j$ Rule $j$.
For a sequence to break Rule $1$, it must contain no $0$s. There are $4^5=1024$ ways to do this.
For a sequence to break Rule $2$ but not Rule $1$, it must contain exactly one $0$, and all other digits must be no less than $2$. After placing the one $0$ in any of $5$ slots, there are $4$ slots left with $3$ options each, giving a total of $5 \times 3^4 = 405$ ways.
For a sequence to break Rule $3$ but neither Rule $2$ or $1$, it must have two digits less than $2$ (either $(0, 0)$ or $(0, 1)$) and all other digits must be $3$ or $4$. There are a total of $\dbinom52+5\times4=30$ ways to arrange the first two digits, and $2^3$ ways to arrange the other three, leaving $30\times2^3=240$ ways to do this.
Finally, for a sequence to only break Rule $4$, it must have three digits less than $3$. They could be $(0, 1, 2)$ with $5\times4\times3=60$ arrangements, or $(0, 1, 1)(0, 0, 1)(0, 0, 2)$ with $5\times\dbinom42=30$ arrangements each, or $(0, 0, 0)$ with $\dbinom53=10$ arrangements. This gives $60+30\times3+10=160$ possible arrangements overall. The remaining two digits must be two 4s.
There are in total $5^5=3125$ possible arrangements, so by adding all of the invalid states together and subtracting from $3125$, we get our answer $3125-(1024+405+240+160)=1296$.
Let $R$, $S$, and $T$ be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the $x$-axis. The left edge of $R$ and the right edge of $S$ are on the $y$-axis, and $R$ contains $\dfrac{9}{4}$ as many lattice points as does $S$. The top two vertices of $T$ are in $R \cup S$, and $T$ contains $\dfrac{1}{4}$ of the lattice points contained in $R \cup S.$ See the figure (not drawn to scale).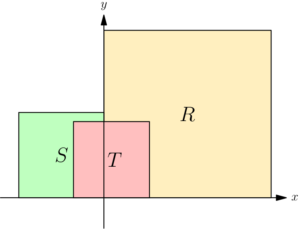
The fraction of lattice points in $S$ that are in $S \cap T$ is $27$ times the fraction of lattice points in $R$ that are in $R \cap T$. What is the minimum possible value of the edge length of $R$ plus the edge length of $S$ plus the edge length of $T$?
$\textbf{(A) }336\qquad\textbf{(B) }337\qquad\textbf{(C) }338\qquad\textbf{(D) }339\qquad\textbf{(E) }340$
$\textbf{B}$
Let $r,s$ and $t$ be the number of lattice points on the side length of square $R,S$ and $T$, respectively. Note that the lengths of the side lengths are the number of lattice points minus $1$, so the sum of side lengths the question asked is $r+s+t-3$. Furthermore, the number of lattice points inside a rectangular region is equal to the number of lattice points in its width times the number of lattice points along its length. Using this fact, the number of lattice points in $R$ is $r^2$, the number of lattice points in $S$ is $s^2$, and the number of lattice points in $T$ is $t^2$.
Now, by the first condition that $R$ contains $\dfrac{9}{4}$ as many lattice points as does $S$, we have\[r^2=\frac{9}{4}\cdot s^2 \implies r = \frac{3}{2}s \quad \quad \quad \quad \quad (1)\]
The second condition, the number of lattice points contained in $T$ is $\dfrac14$ of the number of lattice points contained in $R \cup S$. The number of lattice points in $R \cup S$ is equal to the sum of the lattice points in their individually bounded regions, but the lattice points along the $y$-axis for the full length of square $S$ is shared by both of them, so we need to subtract that out. In all, this condition yields $$t^2 = \frac{1}{4}\cdot(r^2 + s^2 - s )\implies t^2 = \frac{1}{4}\cdot\left(\frac{9}{4}\cdot s^2 + s^2 - s \right)\implies 16t^2= s(13s-4)$$ Note from $(1)$ that $s$ is a multiple of $2$. We can write $s=2j$ and substitute: $$16t^2=2j(26j-4) \implies 4t^2=j(13j-2)$$ Note that $j$ must be divisible by two for the product to be divisible by 4. Thus we make another substitution, $j=2k$:\[4t^2=2k(26k-2) \implies t^2 = k(13k-1) \quad \quad \quad \quad \quad (2)\]
Then we look at the last condition that the fraction of the lattice points inside $S$ that are inside $S \cap T$ is $27$ times the fraction of lattice points inside $R$ that are inside $R \cap T$. Let $x$ be the number of lattice points along the bottom of the rectangle formed by $S \cap T$, and $y$ be the number of lattice points along the bottom of the the rectangle formed by $R \cap T$. Therefore, the number of lattice points in $S\cap T$ is $xt$ and the number of lattice points in $R \cap T$ is $yt$. Thus, by this condition, $$\frac{xt}{s^2} = 27 \cdot \frac{yt}{r^2} \implies \frac{x}{s^2} = 27 \cdot \frac{y}{\frac{9}{4}\cdot s^2} \implies x= 12y$$ Notice that $t=x+y-1$, so we have\[t=x+y-1=12y+y-1=13y-1 \quad \quad \quad \quad \quad (3)\]
Now notice that by $(3)$ , $$t\equiv -1 \pmod{13}\implies t^2 \equiv 1 \pmod{13}$$
However, by $(2)$ , $t^2 \equiv -k \pmod{13}$. Therefore, $$-k \equiv 1 \pmod{13} \implies k \equiv -1 \pmod{13}$$
By Euclids algorithm, the greatest common divisor of $a$ and $b$ is $\gcd(a,b)=\gcd(b, a\mod b)$. Hence, $k$ is relatively prime to $13k-1$ because $$\gcd(13k-1,k)=\gcd(k, 13k-1\mod k)=\gcd(k,-1)=1$$
Therefore, by $(2)$ , we know $k$ must be a perfect square since $k$ is relatively prime to $13k-1$ and the two must multiply to a perfect square. Hence, we know two conditions on $k$, and we can now guess and check to find the smallest that satisfies both.
We check $k=12$ first since its one less than a multiple of $13$, but this does not work. Next, we have $k=25$ which works because $25$ is a perfect square. Thus, we have found the smallest $k$, and therefore the smallest $r, s, t$.
Now we just work backwards: $j= 2k = 50$ and $s=2j=100$. Then $r=\dfrac{3}{2}\times 100 = 150$. By $(2)$ , $t^2=25(13\times25-1) \implies t=90$.
Finally, the sum of the side lengths of each squares is $r+s+t-3=150+100+90-3=337$.