AMC 10 2023 Test A

Instructions

This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.
You will receive 6 points for each correct answer, 2.5 points for each problem left unanswered if the year is before 2006, 1.5 points for each problem left unanswered if the year is after 2006, and 0 points for each incorrect answer.
No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers (and calculators that are accepted for use on the test if before 2006. No problems on the test will require the use of a calculator).
Figures are not necessarily drawn to scale.
You will have 75 minutes working time to complete the test.

Question 1

Cities $A$ and $B$ are $45$ miles apart. Alicia lives in $A$ and Beth lives in $B$. Alicia bikes towards $B$ at $18$ miles per hour. Leaving at the same time, Beth bikes toward $A$ at $12$ miles per hour. How many miles from City $A$ will they be when they meet?

$\textbf{(A) }20\qquad\textbf{(B) }24\qquad\textbf{(C) }25\qquad\textbf{(D) }26\qquad\textbf{(E) }27$

Solution

$\textbf{E}$

The relative speed of Alicia and Beth is $18+12=30$ miles per hour. It takes them $45/30=1.5$ hours to meet each other. The place where they meet is $18\times1.5=27$ miles away from City $A$.

Question 2

The weight of $\dfrac{1}{3}$ of a large pizza together with $3 \dfrac{1}{2}$ cups of orange slices is the same weight of $\dfrac{3}{4}$ of a large pizza together with $\dfrac{1}{2}$ cups of orange slices. A cup of orange slices weigh $\dfrac{1}{4}$ of a pound. What is the weight, in pounds, of a large pizza?

$\textbf{(A) }1\dfrac{4}{5}\qquad\textbf{(B) }2\qquad\textbf{(C) }2\dfrac{2}{5}\qquad\textbf{(D) }3\qquad\textbf{(E) }3\dfrac{3}{5}$

Solution

$\textbf{A}$

Let $x$ and $y$ be the weight of a large pizza and a cup of orange slice in pound, respectively. Hence, we get $$\dfrac13x+3\dfrac12y=\dfrac34x+\dfrac12y\rightarrow x=\dfrac{36}{5}y$$ Given that $y=\dfrac14$, the weight of a large pizza is $x=\dfrac{36}{5}y=\dfrac95=1\dfrac45$ pounds.

Question 3

How many positive perfect squares less than $2023$ are divisible by $5$?

$\textbf{(A) }8\qquad\textbf{(B) }9\qquad\textbf{(C) }10\qquad\textbf{(D) }11\qquad\textbf{(E) }12$

Solution

$\textbf{A}$

If a perfect square is divisible by 5, it is also divisible by $5^2=25$. Hence, the perfect squares are in the form of $5^2, 10^2, 15^2,\cdots$

We know that $45^2=2025$, which is slightly greater than 2023. Therefore, the greatest perfect square which satisfies the condition is $40^2$. The number of elements in the sequence $5^2,10^2,\cdots,40^2$ is $40/5=8$. So the answer is 8.

Question 4

A quadrilateral has all integer side lengths, a perimeter of $26$, and one side of length $4$. What is the greatest possible length of one side of this quadrilateral?

$\textbf{(A) }9\qquad\textbf{(B) }10\qquad\textbf{(C) }11\qquad\textbf{(D) }12\qquad\textbf{(E) }13$

Solution

$\textbf{D}$

Let's use the triangle inequality. We know that for a triangle, the sum of the lengths of two shorter sides must always be longer than the longest side. This is because if the longest side were to be as long as the sum of the other sides, or longer, we would only have a line.

Similarly, for a quadrilateral, the sum of the lengths of the shortest three sides must be longer than the longest side. Thus, the length of the longest side must be shorter than $26/2=13$. So the greatest possible length of one side of this quadrilateral is $12$.

Question 5

How many digits are in the base-ten representation of $8^5 \cdot 5^{10} \cdot 15^5$?

$\textbf{(A) } 14 \qquad\textbf{(B) }15 \qquad\textbf{(C) }16 \qquad\textbf{(D) }17 \qquad\textbf{(E) } 18$

Solution

$\textbf{E}$

Prime factorization of the expression gives $8^5 \times 5^{10} \times 15^5=2^{15}\times3^{5}\times5^{15}=10^{15}\times3^5=243\times10^{15}$, which is 243 followed by 15 0s. So the number of digits is $3+15=18$.

Question 6

An integer is assigned to each vertex of a cube. The value of an edge is defined to be the sum of the values of the two vertices it touches, and the value of a face is defined to be the sum of the values of the four edges surrounding it. The value of the cube is defined as the sum of the values of its six faces. Suppose the sum of the integers assigned to the vertices is $21$. What is the value of the cube?

$\textbf{(A) } 42 \qquad \textbf{(B) } 63 \qquad \textbf{(C) } 84 \qquad \textbf{(D) } 126 \qquad \textbf{(E) } 252$

Solution

$\textbf{D}$

A cube contains 6 faces, a face contains 4 edges, and a edge contains 2 vertices. Hence, the value of the cube is the sum of the values of 6 faces, or the values of $6\times4=24$ edges, or the values of $24\times2=48$ vertices, or $48/8=6$ times the sum of the values of all 8 vertices. So the value of the cube is $6\times21=126$.

There's another way to think about it. Each of the vertices is counted $3$ times because each vertex is shared by three different edges. Each of the edges is counted $2$ times because each edge is shared by two different faces. Since the sum of the integers assigned to all vertices is $21$, the final answer is $21\times3\times2=126$.

Question 7

Janet rolls a standard $6$-sided die $4$ times and keeps a running total of the numbers she rolls. What is the probability that at some point, her running total will equal $3?$

$\textbf{(A) }\dfrac{2}{9}\qquad\textbf{(B) }\dfrac{49}{216}\qquad\textbf{(C) }\dfrac{25}{108}\qquad\textbf{(D) }\dfrac{17}{72}\qquad\textbf{(E) }\dfrac{13}{54}$

Solution

$\textbf{B}$

There are $3$ cases where the running total will equal $3$: one roll, two rolls, or three rolls.

$\textbf{Case 1}$: The chance of rolling a running total of $3$ in exactly one roll, namely $(3)$, is $\dfrac{1}{6}$.

$\textbf{Case 2}$: The chance of rolling a running total of $3$ in exactly two rolls, namely $(1, 2)$ and $(2, 1)$, is $\dfrac{1}{6}\times\dfrac{1}{6}\times2=\dfrac{1}{18}$.

$\textbf{Case 3}$: The chance of rolling a running total of 3 in exactly three rolls, namely $(1, 1, 1)$, is $\dfrac{1}{6}\times\dfrac{1}{6}\times\dfrac{1}{6}=\dfrac{1}{216}$.

Hence, the probability of rolling a running total of 3 is $\dfrac{1}{6}+\dfrac{1}{18}+\dfrac{1}{216}=\dfrac{49}{216}$.

Question 8

Barb the baker has developed a new temperature scale for her bakery called the Breadus scale, which is a linear function of the Fahrenheit scale. Bread rises at $110$ degrees Fahrenheit, which is $0$ degrees on the Breadus scale. Bread is baked at $350$ degrees Fahrenheit, which is $100$ degrees on the Breadus scale. Bread is done when its internal temperature is $200$ degrees Fahrenheit. What is this, in degrees, on the Breadus scale?

$\textbf{(A) }33\qquad\textbf{(B) }34.5\qquad\textbf{(C) }36\qquad\textbf{(D) }37.5\qquad\textbf{(E) }39$

Solution

$\textbf{D}$

Let $x$ be the temperature in degree on the Breadus scale when the temperature is 200 degrees Fahrenheit. Given that there is a linear function between Breadus scale and Fahrenheit scale, we have $$\dfrac{350-200}{200-110}=\dfrac{100-x}{x-0}$$ Solving, we get $x=37.5$.

Question 9

A digital display shows the current date as an $8$-digit integer consisting of a $4$-digit year, followed by a $2$-digit month, followed by a $2$-digit date within the month. For example, Arbor Day this year is displayed as $20230428.$ For how many dates in $2023$ does each digit appear an even number of times in the $8$-digital display for that date?

$\textbf{(A)}~5\qquad\textbf{(B)}~6\qquad\textbf{(C)}~7\qquad\textbf{(D)}~8\qquad\textbf{(E)}~9$

Solution

$\textbf{E}$

There is one $3$ in 2023, so we need one more 3 (three more 3s are impossible for month and day). For the same reason, we need one more $0$.

If $3$ is the units digit of the month, then $0$ must be the tens digit of the month. Therefore, the day must be 11 or 22. There are 2 valid 8-digit integers (20230311 and 20230322) in this case.

If $3$ is the tens digit of the day, then the units digit of the day must be 0 or 1. When the day is 30, the only possible number for month is 11. When the day is 31, the month could be 01 or 10. There are 3 valid 8-digit integers (20231130, 20230131 and 20231031) in this case.

If $3$ is the units digit of the day, then $0$ could go in any of the $3$ remaining slots. If 0 is the tens digit of the day, then the month must be $11$. If $0$ is the units digit of the month, then the other two slots must both be $1$. If $0$ is the tens digit of the month, then the other two slots can be either both $1$ or both $2$. There are $4$ valid 8-digit integers (20231103, 20231013, 20230113 and 20230223) in this case.

In total, we have $2+3+4=9$ valid 8-digit integers.

Question 10

Maureen is keeping track of the mean of her quiz scores this semester. If Maureen scores an $11$ on the next quiz, her mean will increase by $1$. If she scores an $11$ on each of the next three quizzes, her mean will increase by $2$. What is the mean of her quiz scores currently?

$\textbf{(A) }4\qquad\textbf{(B) }5\qquad\textbf{(C) }6\qquad\textbf{(D) }7\qquad\textbf{(E) }8$

Solution

$\textbf{D}$

Let $a$ represent the amount of tests taken previously and $x$ the mean of the scores currently.

We can write the following equations:\[\frac{ax+11}{a+1}=x+1\qquad (1)\]\[\frac{ax+33}{a+3}=x+2\qquad (2)\] Multiplying equation $(1)$ by $(a+1)$ and solving, we get:\[ax+11=ax+a+x+1\]\[11=a+x+1\]\[a+x=10\qquad (3)\]Multiplying equation $(2)$ by $(a+3)$ and solving, we get:\[ax+33=ax+2a+3x+6\]\[33=2a+3x+6\]\[2a+3x=27\qquad (4)\]
Solving the system of equations for $(3)$ and $(4)$, we find that $a=3$ and $x=7$. The answer is 7.

Question 11

A square of area $2$ is inscribed in a square of area $3$, creating four congruent triangles, as shown below. What is the ratio of the shorter leg to the longer leg in the shaded right triangle?

$\textbf{(A) }\dfrac15\qquad\textbf{(B) }\dfrac14\qquad\textbf{(C) }2-\sqrt3\qquad\textbf{(D) }\sqrt3-\sqrt2\qquad\textbf{(E) }\sqrt2-1$

Solution

$\textbf{C}$

Let $a,b$ be the lengths of the shorter leg and the longer leg of the shaded right triangle, respectively. By the Pythagorean Theorem, the length of the hypotenuse of the triangle is $\sqrt{a^2+b^2}$. Hence, the area of the smaller square is $$a^2+b^2=2\qquad(1)$$ The side length of the larger square is $a+b$, so its area is $$(a+b)^2=3\qquad(2)$$ Subtracting (1) from (2), we get $$2ab=1\qquad(3)$$ Dividing (1) by (3), we get $$\dfrac{a}{2b}+\dfrac{b}{2a}=2$$ where $\dfrac{a}{b}=r$ is the ratio we are looking for. Substituting and simplifying, we have $$r+\dfrac{1}{r}=4$$ Solving, we get the answer $r=2-\sqrt3$.

Question 12

How many three-digit positive integers $N$ satisfy the following properties?

$\bullet\quad$ The number $N$ is divisible by $7$.$\newline$
$\bullet\quad$ The number formed by reversing the digits of $N$ is divisible by $5$.

$\textbf{(A) } 13 \qquad \textbf{(B) } 14 \qquad \textbf{(C) } 15 \qquad \textbf{(D) } 16 \qquad \textbf{(E) } 17$

Solution

$\textbf{B}$

Multiples of $5$ will always end in $0$ or $5$. Since $N$ is a three-digit positive integer, it cannot start with 0, narrowing our choices to three-digit numbers starting with $5$. Given that the numbers must be divisible by 7, all possibilities have to be in the range from $7 \times 72=504$ to $7 \times 85=595$ inclusive. Hence, the number of integer $N$ which satisfy such conditions is $85 - 72 + 1 = 14$.

Question 13

Abdul and Chiang are standing $48$ feet apart in a field. Bharat is standing in the same field as far from Abdul as possible so that the angle formed by his lines of sight to Abdul and Chiang measures $60^\circ$. What is the square of the distance (in feet) between Abdul and Bharat?

$\textbf{(A) } 1728 \qquad \textbf{(B) } 2601 \qquad \textbf{(C) } 3072 \qquad \textbf{(D) } 4608 \qquad \textbf{(E) } 6912$

Solution

$\textbf{C}$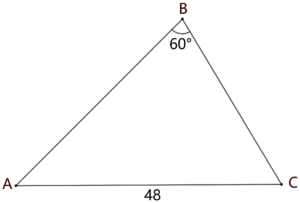

Let points $A,B,C$ be the positions of Abdul, Bharat and Chiang, respectively.

We know that $AC=48$, $\angle B=60^\circ$, and we are looking for the maximum value of $AB$. By the Law of Sines, we have $\dfrac{AB}{\sin\angle C}=\dfrac{AC}{\sin\angle B}$. Hence, we get $$AB=AC\cdot\dfrac{\sin\angle C}{\sin\angle B}=48\cdot\dfrac{\sin\angle C}{\sin60^\circ}=32\sqrt3\sin\angle C$$ The maximum of $\sin\angle C$ is 1, where $\angle C=90^\circ$. Therefore, the maximum value of $AB$ is $32\sqrt3$. The answer is $\left(32\sqrt3\right)^2=3072$.

Question 14

A number is chosen at random from among the first $100$ positive integers, and a positive integer divisor of that number is then chosen at random. What is the probability that the chosen divisor is divisible by $11$?

$\textbf{(A)}~\dfrac{4}{100}\qquad\textbf{(B)}~\dfrac{9}{200} \qquad \textbf{(C)}~\dfrac{1}{20} \qquad\textbf{(D)}~\dfrac{11}{200}\qquad\textbf{(E)}~\dfrac{3}{50}$

Solution

$\textbf{B}$

In order for the divisor chosen to be a multiple of $11$, the original number chosen must also be a multiple of $11$. Among the first $100$ positive integers, there are 9 multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99.

Because all of these numbers are multiples of $11$ to the first power and first power only, their factors can either have $11$ as a factor ($11^{1}$) or not have $11$ as a factor ($11^{0}$), resulting in a $\dfrac{1}{2}$ chance of a factor chosen being divisible by $11$.

The chance of choosing these 9 multiples of $11$ under $100$ is $\dfrac{9}{100}$, so the final answer is $\dfrac{9}{100} \times \dfrac{1}{2} =\dfrac{9}{200}.$

Question 15

An even number of circles are nested, starting with a radius of $1$ and increasing by $1$ each time, all sharing a common point. The region between every other circle is shaded, starting with the region inside the circle of radius $2$ but outside the circle of radius $1.$ An example showing $8$ circles is displayed below. What is the least number of circles needed to make the total shaded area at least $2023\pi$?

$\textbf{(A) } 46 \qquad \textbf{(B) } 48 \qquad \textbf{(C) } 56 \qquad \textbf{(D) } 60 \qquad \textbf{(E) } 64$

Solution

$\textbf{E}$

Let $n$ be the least number of circles needed. If $n$ is odd, then the $n$th circle is unnecessary because it brings no extra shaded area. Hence, $n$ must be even. The area of the shaded region is \begin{align*}
A&=\pi(2^2-1^2)+\pi(4^2-3^3)+\cdots+\pi\left[n^2-(n-1)^2\right]\\
&=\pi(2+1)(2-1)+\pi(4+3)(4-3)+\cdots+\pi\left[n+(n-1)\right]\left[n-(n-1)\right]\\
&=\pi(1+2+3+4+\cdots+n)\\
&=\dfrac12n(n+1)\pi\\
&\geq2023\pi
\end{align*} Therefore, we get $$n(n+1)\geq4046$$ For the answer choices, we see that $60\times61<4046$ and $64\times65>4046$. So the answer is E.

Question 16

In a table tennis tournament every participant played every other participant exactly once. Although there were twice as many right-handed players as left-handed players, the number of games won by left-handed players was $40\%$ more than the number of games won by right-handed players. (There were no ties and no ambidextrous players.) What is the total number of games played?

$\textbf{(A) }15\qquad\textbf{(B) }36\qquad\textbf{(C) }45\qquad\textbf{(D) }48\qquad\textbf{(E) }66$

Solution

$\textbf{B}$

Let the number of left-handed players be $n$, so the number of right-handed players is $2n$.

The number of games won by the left-handed players comes in two ways:

$\bullet\quad$ The games played by two left-left pairs, which is $\dbinom{n}{2}=\dfrac{n(n-1)}{2}$, and$\newline$
$\bullet\quad$ The games played by left-right pairs, which we call it $x$.

Note that $x\leq 2n^2,$ which is the total number of games played by left-right pairs.

Using the same logic for the number of games won by the right-handed players, it also comes in two ways:

$\bullet\quad$ The games played by two right-right pairs, which is $\dbinom{2n}{2}=n(2n-1)$, and$\newline$
$\bullet\quad$ The games played by left-right pairs, which is $2n^2-x$.

Hence, we have \[\dfrac{\dfrac{n(n-1)}{2}+x}{n(2n-1)+2n^2-x}=1.4\]which gives\[x=\frac{17n^2}{8}-\frac{3n}{8}\]We know that $x\leq 2n^2$, which leads to \begin{align*} \frac{17n^2}{8}-\frac{3n}{8} &\le 2n^2 \\ 17n^2 - 3n &\le 16n^2 \\ n^2 - 3n &\le 0 \\ n &\le 3 \end{align*} So the total number of players $3n$ can only be $3$, $6$, and $9$.

The total number of games $\dbinom{3n}{2}=\dfrac{3n(3n-1)}{2}$ must be a multiple of $1+1.4=2.4$. Among $\{3,6,9\}$, only $3n = 9$ satisfies this condition. So the total number of games is $\dfrac{9\times8}{2} = 36.$

Question 17

Let $ABCD$ be a rectangle with $AB = 30$ and $BC = 28$. Point $P$ and $Q$ lie on $\overline{BC}$ and $\overline{CD}$ respectively so that all sides of $\triangle{ABP}, \triangle{PCQ},$ and $\triangle{QDA}$ have integer lengths. What is the perimeter of $\triangle{APQ}$?

$\textbf{(A) } 84 \qquad \textbf{(B) } 86 \qquad \textbf{(C) } 88 \qquad \textbf{(D) } 90 \qquad \textbf{(E) } 92$

Solution

$\textbf{A}$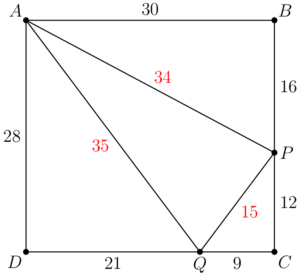

We know that all side lengths are integers, so we can test Pythagorean triples for all triangles.

First, we focus on $\triangle{ABP}$. The length of $AB$ is $30$, and the possible (small enough) Pythagorean triples $\triangle{ABP}$ can be are $(3, 4, 5), (5, 12, 13), (8, 15, 17),$ where the length of the longer leg must be a factor of $30$. Testing these, we see that only $(8, 15, 17)$ is a valid solution. Thus, we know that $BP = 16$ and $AP = 34$.

Next, we move on to $\triangle{QDA}$. The length of $AD$ is $28$, and the small enough triples are $(3, 4, 5)$ and $(7, 24, 25)$. The length of the longer leg must be a factor of 28. Testing again, we see that $(3, 4, 5)$ is our triple. We get the value of $DQ = 21$, and $AQ = 35$.

Hence, we get $CQ = CD - DQ=30-21=9$ and $CP = BC - BP=28-16=12$. We see that $\triangle{CPQ}$ is a right triangle with side length ratios $(3,4,5)$, and the hypotenuse $PQ$ is equal to $15$.

$\triangle{APQ}$ has side lengths $34, 35,$ and $15,$ so its perimeter is $34 + 35 + 15 = 84.$

Question 18

A rhombic dodecahedron is a solid with $12$ congruent rhombus faces. At every vertex, $3$ or $4$ edges meet, depending on the vertex. How many vertices have exactly $3$ edges meet?

$\textbf{(A) }5\qquad\textbf{(B) }6\qquad\textbf{(C) }7\qquad\textbf{(D) }8\qquad\textbf{(E) }9$

Solution

$\textbf{D}$

According to Euler's formula, $$\text{Vertices}+\text{Faces}-\text{Edges}=2$$ We know that there are $12$ faces. The number of edges is 24, because there are 12 faces each with four edges and each edge is shared by two faces. Now we know that there are $2-12+24=14$ vertices.

Let $x$ be the number of vertices with $3$ edges. Then we know there are $14-x$ vertices with 4 edges. The number of edges is $\dfrac{3x+4(14-x)}{2}=24$ because each edge connects two vertices. Solving, we get $x = 8$.

Question 19

The line segment formed by $A(1, 2)$ and $B(3, 3)$ is rotated to the line segment formed by $A'(3, 1)$ and $B'(4, 3)$ about the point $P(r, s)$. What is $|r-s|$?

$\textbf{(A) } \dfrac{1}{4} \qquad \textbf{(B) } \dfrac{1}{2} \qquad \textbf{(C) } \dfrac{3}{4} \qquad \textbf{(D) } \dfrac{2}{3} \qquad \textbf{(E) } 1$

Solution

$\textbf{E}$

Due to rotations preserving distance, we have $AP = A^\prime P$ and $BP = B^\prime P$. From here, we see that $P$ must be on the perpendicular bisector of $\overline{AA^\prime}$ due to the property of perpendicular bisectors keeping the distance to two points constant. Similarly, $P$ is also a point on the perpendicular bisector of $\overline{BB^\prime}$. Hence, we see that $P$ is the intersection of these two perpendicular bisectors.

Firstly, we need to find the perpendicular bisector of $\overline{AA^\prime}$. The slope of $\overline{AA^\prime}$ is $\dfrac{1-2}{3-1} = -\dfrac12$. Hence, the slope of the perpendicular bisector of $\overline{AA^\prime}$ is $2$, because the product of the slopes of two perpendicular lines is $-1$. The midpoint of $AA^\prime$ is $(2, \dfrac32)$. Therefore, the equation of the perpendicular bisector of $\overline{AA^\prime}$ is $y = 2x - \dfrac52$.

Then we proceed to find the perpendicular bisector of $\overline{BB^\prime}$. We see that $\overline{BB^\prime}$ is just a horizontal line segment with midpoint at $(3.5, 3)$. This means that the equation of the perpendicular bisector of $\overline{BB^\prime}$ is $x = 3.5$.

Point $P$ is the intersection of these two perpendicular bisectors, meaning that it has to satisfy both equations. Plugging $x=3.5$ into $y = 2x - \dfrac52$, we find that $y=4.5$. So the coordinate of point $P(r,s)$ is $(3.5,4.5)$. Hence, the answer is $|r - s| = |3.5 - 4.5| =1$.

Question 20

Each square in a $3\times3$ grid of squares is colored red, white, blue, or green so that every $2\times2$ square contains one square of each color. One such coloring is shown on the right below. How many different colorings are possible?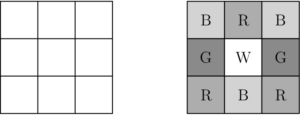

$\textbf{(A) }24\qquad\textbf{(B) }48\qquad\textbf{(C) }60\qquad\textbf{(D) }72\qquad\textbf{(E) }96$

Solution

$\textbf{D}$

There are $4!=24$ ways to color the top-left $2\times2$ square. Next, we fill out the bottom-right corner square. In the bottom-right $2\times2$ square, one corner is already filled (the central square) from our initial coloring, so we have 3 color options for the bottom-right corner square. Now considering the remaining squares, all of these only have one way to be filled. Thus, the total number of ways is $24\times3=72$.

Question 21

Let $P(x)$ be the unique polynomial of minimal degree with the following properties:

$\bullet\quad$$P(x)$ has a leading coefficient $1$,$\newline$
$\bullet\quad$$1$ is a root of $P(x)-1$,$\newline$
$\bullet\quad$$2$ is a root of $P(x-2)$,$\newline$
$\bullet\quad$$3$ is a root of $P(3x)$, and$\newline$
$\bullet\quad$$4$ is a root of $4P(x)$.

The roots of $P(x)$ are integers, with one exception. The root that is not an integer can be written as $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime integers. What is $m+n$?

$\textbf{(A) }41\qquad\textbf{(B) }43\qquad\textbf{(C) }45\qquad\textbf{(D) }47\qquad\textbf{(E) }49$

Solution

$\textbf{D}$

According to the properties of the polynomial, we find $P(2-2)=0$, $P(9)=0$ and $4P(4)=0$. Therefore, we know that $0$, $9$, and $4$ are roots of the polynomial. Hence, we can factor $P(x)$ as $$P(x)=x(x - 4)(x - 9)(x - r)$$ where $r=\dfrac{m}{n}$ is the non-integer root.

By properties 2, we see that $P(1)-1=0$. So we have $$1\times(1-4)\times(1-9)\times(1-r)=1$$ Solving, we get $r = \dfrac{23}{24}$. So the answer is $23 + 24 = 47$.

Question 22

Circle $C_1$ and $C_2$ each have radius $1$, and the distance between their centers is $\dfrac{1}{2}$. Circle $C_3$ is the largest circle internally tangent to both $C_1$ and $C_2$. Circle $C_4$ is internally tangent to both $C_1$ and $C_2$ and externally tangent to $C_3$. What is the radius of $C_4$?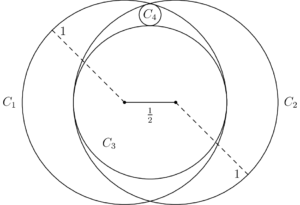

$\textbf{(A) } \dfrac{1}{14} \qquad \textbf{(B) } \dfrac{1}{12} \qquad \textbf{(C) } \dfrac{1}{10} \qquad \textbf{(D) } \dfrac{3}{28} \qquad \textbf{(E) } \dfrac{1}{9}$

Solution

$\textbf{D}$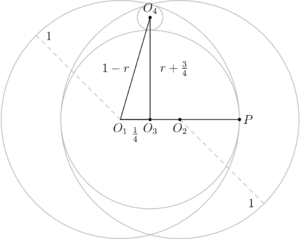

Let $O_1,O_2$ be the centers of circle $C_1$ and $C_2$, respectively. Then we have $O_1O_2=\dfrac12$. By symmetry, the midpoint of line segment $O_1O_2$ is the center of circle $C_3$. Let's call it $O_3$.

Let the point of tangency of circle $O_1$ and $O_3$ be $P$.Then we have $$O_3P = O_2O_3 + O_2P = O_2O_3 + O_1P-O_1O_2=\dfrac14+1-\dfrac12=\dfrac{3}{4}$$ So the radius of circle $C_3$ is $\dfrac34$.

Let $O_4$ be the center of circle $C_4$, and $r$ be the radius of circle $C_4$. By symmetry, we see that $O_3O_4\perp O_1O_2$. In right triangle $O_1O_3O_4$, we have $O_1O_3=\dfrac14$, $O_3O_4=r+\dfrac34$, and $O_1O_4=1-r$. By the Pythagorean theorem, we have $$\left(\dfrac14\right)^2+\left(r+\dfrac34\right)^2=(1-r)^2$$ Solving, we get $r =\dfrac{3}{28}$.

Question 23

If the positive integer $c$ has positive integer divisors $a$ and $b$ with $c = ab$, then $a$ and $b$ are said to be $\textit{complementary}$ divisors of $c$. Suppose that $N$ is a positive integer that has one complementary pair of divisors that differ by $20$ and another pair of complementary divisors that differ by $23$. What is the sum of the digits of $N$?

$\textbf{(A) } 9 \qquad \textbf{(B) } 13\qquad \textbf{(C) } 15 \qquad \textbf{(D) } 17 \qquad \textbf{(E) } 19$

Solution

$\textbf{C}$

Let $(a,a+20)$ be a pair of complementary divisors of $N$. Since there is another pair of divisors that multiply to $N$ but have a difference of 23, one divisor must be slightly greater than $a+20$, and the other must be slightly less than $a$. Thus, we have two cases \begin{align*}
a(a+20) &= (a-1)(a+22)\\
a(a+20) &= (a-2)(a+21)
\end{align*} Solving the first equation, we get $a=22$. In this case $N=22\times42=924$. The sum of its digits is $9+2+4=15$.

Solving the second equation, we get $a=-42$, which is invalid.

Therefore, the answer is 15.

Question 24

Six regular hexagonal blocks of side length $1$ unit are arranged inside a regular hexagonal frame. Each block lies along an inside edge of the frame and is aligned with two other blocks, as shown in the figure below. The distance from any corner of the frame to the nearest vertex of a block is $\dfrac{3}{7}$ unit. What is the area of the region inside the frame not occupied by the blocks?

$\textbf{(A)}~\dfrac{13 \sqrt{3}}{3}\qquad\textbf{(B)}~\dfrac{216 \sqrt{3}}{49}\qquad\textbf{(C)}~\dfrac{9 \sqrt{3}}{2} \qquad\textbf{(D)}~ \dfrac{14 \sqrt{3}}{3}\qquad\textbf{(E)}~\dfrac{243 \sqrt{3}}{49}$

Solution

$\textbf{C}$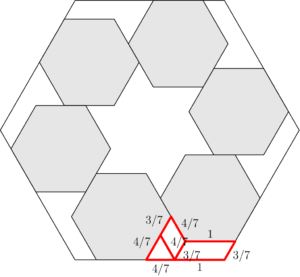

We see that the length of the bottom edge of the hexagonal frame is $\dfrac37+1+\dfrac47+1=3$. The area of the region inside the frame not occupied by the blocks is the area of the hexagonal frame subtracts the areas of 6 hexagonal blocks. Note that the area of a regular hexagon with side length $a$ is the sum of the areas of 6 equilateral triangles with side length $a$, and the area of each triangle is $\dfrac{\sqrt3}{4}a^2$. Thus, the area of a regular hexagon with side length $a$ is $6\times\dfrac{\sqrt3}{4}a^2=\dfrac{3\sqrt3}{2}a^2$. The answer is $$\dfrac{3\sqrt3}{2}\times3^2-6\times\left(\dfrac{3\sqrt3}{2}\times1^2\right)=\dfrac92\sqrt3$$

Question 25

If $A$ and $B$ are vertices of a polyhedron, define the distance $d(A, B)$ to be the minimum number of edges of the polyhedron one must traverse in order to connect $A$ and $B$. For example, $\overline{AB}$ is an edge of the polyhedron, then $d(A, B) = 1$, but if $\overline{AC}$ and $\overline{CB}$ are edges and $\overline{AB}$ is not an edge, then $d(A, B) = 2$. Let $Q$, $R$, and $S$ be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of $20$ equilateral triangles). What is the probability that $d(Q, R) > d(R, S)$?

$\textbf{(A) }\dfrac{7}{22}\qquad\textbf{(B) }\dfrac{1}{3}\qquad\textbf{(C) }\dfrac{3}{8}\qquad\textbf{(D) }\dfrac{5}{12}\qquad\textbf{(E) }\dfrac{1}{2}$

Solution

$\textbf{A}$

By symmetry, the probability $p$ that $d(Q, R) > d(R, S)$ is the same as $d(Q, R) < d(R, S)$. Therefore, we want to find the probability $p^\prime$ that $d(Q, R) = d(R, S)$, then we have $p=\dfrac{1-p^\prime}2$.

To find the total amount of vertices we first find the amount of edges. There are 20 faces, each with 3 edges, and each edge is shared by 2 faces. So the total amount of edge is $\dfrac{20 \times 3}{2}=30$. Next, to find the amount of vertices we can use Euler's formula, $\text{Vertices}+\text{Faces}-\text{Edges}= 2$, and therefore the amount of vertices is $12$.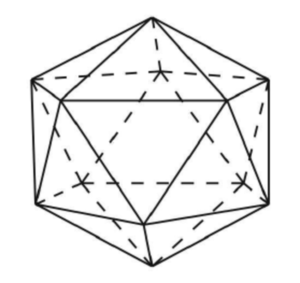

Imagining the icosahedron as having 4 layers. 1 vertex at the top, 5 vertices below connected to the top vertex, 5 vertices below that are 2 edges away from the top vertex, and 1 vertex at the bottom that is 3 edges away from the top.

WLOG, supposing that R is the vertex at the top. If $d(Q, R) = d(R, S)$, there are 2 cases:

$\textbf{Case 1}$: Both $Q$ and $S$ are on the second layer. The probability of this case is $\dfrac{\dbinom52}{\dbinom{11}{2}}=\dfrac{2}{11}$.

$\textbf{Case 2}$: Both $Q$ and $S$ are on the third layer. The probability of this case is the same as Case 1.

Therefore, the probability that $d(Q, R) = d(R, S)$ is $p^\prime=\dfrac{2}{11}\times2=\dfrac{4}{11}$. So the probability that $d(Q, R) > d(R, S)$ is $p=\dfrac{1-p^\prime}2=\dfrac{7}{22}$.