AMC 12 2022 Test A
Instructions
- This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.
- You will receive 6 points for each correct answer, 2.5 points for each problem left unanswered if the year is before 2006, 1.5 points for each problem left unanswered if the year is after 2006, and 0 points for each incorrect answer.
- No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers (and calculators that are accepted for use on the test if before 2006. No problems on the test will require the use of a calculator).
- Figures are not necessarily drawn to scale.
- You will have 75 minutes working time to complete the test.
What is the value of\[3+\frac{1}{3+\frac{1}{3+\frac13}}?\]$\textbf{(A)}\ \dfrac{31}{10}\qquad\textbf{(B)}\ \dfrac{49}{15}\qquad\textbf{(C)}\ \dfrac{33}{10}\qquad\textbf{(D)}\ \dfrac{109}{33}\qquad\textbf{(E)}\ \dfrac{15}{4}$
$\textbf{D}$
\begin{align*}
3+\frac{1}{3+\frac{1}{3+\frac13}} &= 3+\frac{1}{3+\frac{1}{\frac{10}{3}}} \\
&= 3+\frac{1}{3+\frac{3}{10}} \\
&= 3+\frac{1}{\frac{33}{10}} \\
&= 3+\frac{10}{33} \\
&=\frac{109}{33}
\end{align*}
The sum of three numbers is $96.$ The first number is $6$ times the third number, and the third number is $40$ less than the second number. What is the absolute value of the difference between the first and second numbers?
$\textbf{(A) } 1 \qquad \textbf{(B) } 2 \qquad \textbf{(C) } 3 \qquad \textbf{(D) } 4 \qquad \textbf{(E) } 5$
$\textbf{E}$
Let $x$ be the third number. It follows that the first number is $6x,$ and the second number is $x+40.$ We have \[6x+(x+40)+x=8x+40=96\] from which $x=7.$
Therefore, the first number is $42,$ and the second number is $47.$ The absolute value of the difference is $|42-47|=5$.
Five rectangles, $A$, $B$, $C$, $D$, and $E$, are arranged in a square as shown below. These rectangles have dimensions $1\times6$, $2\times4$, $5\times6$, $2\times7$, and $2\times3$, respectively. (The figure is not drawn to scale.) Which of the five rectangles is the shaded one in the middle?
$\textbf{(A) }A\qquad\textbf{(B) }B \qquad\textbf{(C) }C \qquad\textbf{(D) }D\qquad\textbf{(E) }E$
$\textbf{B}$
The area of the square is equal to the sum of the areas of these five rectangles, which is $1\times6+2\times4+5\times6+2\times7+2\times3=64$. Hence, the side length of the square is 8.
For the four rectangles which are not shaded, each of these rectangles has one length and one width located on the side of the square. Therefore, the sum of the perimeters of these four rectangles is twice the perimeter of the square, which is $2\times4\times8=64$. However, we see that the sum of the perimeters of all five rectangles is $2(1+6+2+4+5+6+2+7+2+3)=76$. So the perimeter of the shaded rectangle should be $76-64=12$. The only possible rectangle is $B$.
The least common multiple of a positive integer $n$ and $18$ is $180$, and the greatest common divisor of $n$ and $45$ is $15$. What is the sum of the digits of $n$?
$\textbf{(A) } 3 \qquad \textbf{(B) } 6 \qquad \textbf{(C) } 8 \qquad \textbf{(D) } 9 \qquad \textbf{(E) } 12$
$\textbf{B}$
Note that \begin{align*}
18 &= 2\times3^2\\
180 &= 2^2\times3^2\times5\\
45 &= 3^2\times5 \\
15 &= 3\times5
\end{align*} Let $n = 2^a\times3^b\times5^c.$
From the least common multiple condition, we have\[\operatorname{lcm}(n,18) = \operatorname{lcm}(2^a\times3^b\times5^c,2\times3^2) = 2^{\max(a,1)}\times3^{\max(b,2)}\times5^{\max(c,0)} = 2^2\times3^2\times5\]from which $a=2, b\in\{0,1,2\},$ and $c=1.$
From the greatest common divisor condition, we have\[\gcd(n,45) = \gcd(2^2\times3^b\times5,3^2\times5) = 2^{\min(2,0)}\times3^{\min(b,2)}\times5^{\min(1,1)} = 3\times5\]from which $b=1.$
Together, we conclude that $n=2^2\times3\times5=60.$ The sum of its digits is $6+0=6.$
The $\textit{taxicab distance}$ between points $(x_1, y_1)$ and $(x_2, y_2)$ in the coordinate plane is given by\[|x_1 - x_2| + |y_1 - y_2|.\]For how many points $P$ with integer coordinates is the taxicab distance between $P$ and the origin less than or equal to $20$?
$\textbf{(A)} \, 441 \qquad\textbf{(B)} \, 761 \qquad\textbf{(C)} \, 841 \qquad\textbf{(D)} \, 921 \qquad\textbf{(E)} \, 924$
$\textbf{C}$
Let $(x,y)$ be the coordinate of point $P$.
If $y=0$, then $x$ varies from $-20$ to $+20$, which gives $20+20+1=41$ valid points.
If $y=\pm1$, then $x$ varies from $-19$ to $+19$, which gives $2\times(19+19+1)=2\times39$ valid points.
If $y=\pm2$, then $x$ varies from $-18$ to $+18$, which gives $2\times(18+18+1)=2\times37$ valid points.
$\cdots$
If $y=\pm20$, then $x$ must be 0, which gives $2\times1$ valid points.
Hence, the total number of points is $$41+2(1+3+\cdots+39)=41+2\times\dfrac{(1+39)\times20}{2}=841$$
A data set consists of $6$ (not distinct) positive integers: $1$, $7$, $5$, $2$, $5$, and $X$. The average (arithmetic mean) of the $6$ numbers equals a value in the data set. What is the sum of all possible values of $X$?
$\textbf{(A) } 10 \qquad \textbf{(B) } 26 \qquad \textbf{(C) } 32 \qquad \textbf{(D) } 36 \qquad \textbf{(E) } 40$
$\textbf{D}$
The average of the 6 numbers is $\dfrac{1+7+5+2+5+X}{6}=\dfrac{X+20}{6}$. The average could be equal to 1, 2, 5, 7 or $X$. Hence, we get 5 equations $$\dfrac{X+20}{6}=1, 2, 5, 7 \text{ or } X$$ Solving, we get $X=-14, -8, 10, 22 \text{ or } 4$. Since $X$ is a positive integer, only 10, 22 and 4 are possible values of $X$. The answer is $10+22+4=36$.
A rectangle is partitioned into $5$ regions as shown. Each region is to be painted a solid color - red, orange, yellow, blue, or green - so that regions that touch are painted different colors, and colors can be used more than once. How many different colorings are possible?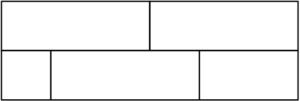
$\textbf{(A) }120\qquad\textbf{(B) }270\qquad\textbf{(C) }360\qquad\textbf{(D) }540\qquad\textbf{(E) }720$
$\textbf{D}$
The top-left region has 5 coloring choices. Then the top-right region has 4 coloring choices, and the middle region in the bottom row has 3 coloring choices. Now both the bottom-left and bottom-right regions each have 3 coloring choices. Therefore, the total number of coloring arrangements is $5\times4\times3\times3\times3=540$.
The infinite product\[\sqrt[3]{10} \cdot \sqrt[3]{\sqrt[3]{10}} \cdot \sqrt[3]{\sqrt[3]{\sqrt[3]{10}}} \cdots\]evaluates to a real number. What is that number?
$\textbf{(A) }\sqrt{10}\qquad\textbf{(B) }\sqrt[3]{100}\qquad\textbf{(C) }\sqrt[4]{1000}\qquad\textbf{(D) }10\qquad\textbf{(E) }10\sqrt[3]{10}$
$\textbf{A}$
\[\sqrt[3]{10} \cdot \sqrt[3]{\sqrt[3]{10}} \cdot \sqrt[3]{\sqrt[3]{\sqrt[3]{10}}} \cdots=10^{\frac13}\cdot10^{\frac{1}{3^2}}\cdot10^{\frac{1}{3^3}}\cdots=10^{\frac13+\frac{1}{3^2}+\frac{1}{3^3}+\cdots}\] Let $S$ be the sum of infinite geometric series $\dfrac13+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\cdots$ Hence, we have \begin{align*}
S&=\ \ \ \ \ \dfrac13+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\cdots\qquad(1)\\
3S&=1+\dfrac13+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\cdots\qquad(2)
\end{align*} Subtracting equation (1) from equation (2), we get $$2S=1\rightarrow S=\dfrac12$$ So the answer is $10^{\frac12}=\sqrt{10}$.
On Halloween $31$ children walked into the principal's office asking for candy. They can be classified into three types: Some always lie; some always tell the truth; and some alternately lie and tell the truth. The alternaters arbitrarily choose their first response, either a lie or the truth, but each subsequent statement has the opposite truth value from its predecessor. The principal asked everyone the same three questions in this order.
“Are you a truth-teller?” The principal gave a piece of candy to each of the $22$ children who answered yes.
“Are you an alternater?” The principal gave a piece of candy to each of the $15$ children who answered yes.
“Are you a liar?” The principal gave a piece of candy to each of the $9$ children who answered yes.
How many pieces of candy in all did the principal give to the children who always tell the truth?
$\textbf{(A) } 7 \qquad \textbf{(B) } 12 \qquad \textbf{(C) } 21 \qquad \textbf{(D) } 27 \qquad \textbf{(E) } 31$
$\textbf{A}$
Note that:
$\bullet$ Truth-tellers would answer yes-no-no to the three questions in this order.$\newline$
$\bullet$ Liars would answer yes-yes-no to the three questions in this order.$\newline$
$\bullet$ Alternaters who responded truth-lie-truth would answer no-no-no to the three questions in this order.$\newline$
$\bullet$ Alternaters who responded lie-truth-lie would answer yes-yes-yes to the three questions in this order.
Suppose that there are $T$ truth-tellers, $L$ liars, and $A$ alternaters who responded lie-truth-lie.
The conditions of the first two questions imply that \begin{align*}
T+L+A&=22\\
L+A&=15
\end{align*} Subtracting the second equation from the first, we have $T=22-15=7$. Since the truth-tellers answer yes to the first question only, they get 7 pieces of candy in total.
The condition of the third question is superfluous for this question.
How many ways are there to split the integers $1$ through $14$ into $7$ pairs such that in each pair, the greater number is at least $2$ times the lesser number?
$\textbf{(A) } 108 \qquad \textbf{(B) } 120 \qquad \textbf{(C) } 126 \qquad \textbf{(D) } 132 \qquad \textbf{(E) } 144$
$\textbf{E}$
Clearly, the integers from $8$ through $14$ must be in different pairs, so are the integers from $1$ through $7.$
$7$ must pair with $14.$$\newline$
When the position of 7 is confirmed, $6$ can pair with either $12$ or $13.$$\newline$
When the position of 6 is confirmed, $5$ can pair with any of the three remaining numbers from $10,11,12,13.$$\newline$
Finaly, $1,2,3,4$ can pair with the other four remaining numbers from $8,9,10,11,12,13$ without restrictions.
Hence, the total number of arrangements is $1\times2\times3\times4!=144$.
What is the product of all real numbers $x$ such that the distance on the number line between $\log_6x$ and $\log_69$ is twice the distance on the number line between $\log_610$ and $1$?
$\textbf{(A) } 10 \qquad \textbf{(B) } 18 \qquad \textbf{(C) } 25 \qquad \textbf{(D) } 36 \qquad \textbf{(E) } 81$
$\textbf{E}$
Notice that there must be two such real numbers $x$: one greater than $\log_69$ and one less than it. Let these two numbers be $x_1$ and $x_2$, where $x_1>x_2$. Hence, we have $$\log_6x_1-\log_69=\log_69-\log_6x_2=2(\log_610 - 1)$$ $$\log_6x_1+\log_6x_2=2\log_69$$ $$\log_6x_1x_2=\log_69^2$$ So the product of all real numbers $x$ is $x_1x_2=9^2=81$.
Let $M$ be the midpoint of $\overline{AB}$ in regular tetrahedron $ABCD$. What is $\cos(\angle CMD)$?
$\textbf{(A) } \dfrac14 \qquad \textbf{(B) } \dfrac13 \qquad \textbf{(C) } \dfrac25 \qquad \textbf{(D) } \dfrac12 \qquad \textbf{(E) } \dfrac{\sqrt{3}}{2}$
$\textbf{B}$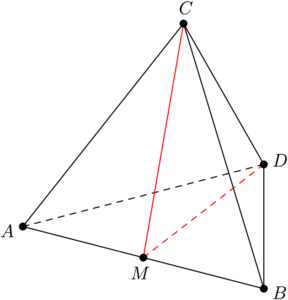
Without loss of generality, let the edge-length of $ABCD$ be $2.$ It follows that $CM=DM=\sqrt3.$
By the Law of Cosines,\[\cos(\angle CMD) = \frac{CM^2 + DM^2 - CD^2}{2(CM)(DM)} = \frac13\]
Let $\mathcal{R}$ be the region in the complex plane consisting of all complex numbers $z$ that can be written as the sum of complex numbers $z_1$ and $z_2$, where $z_1$ lies on the segment with endpoints $3$ and $4i$, and $z_2$ has magnitude at most $1$. What integer is closest to the area of $\mathcal{R}$?
$\textbf{(A) } 13 \qquad \textbf{(B) } 14 \qquad \textbf{(C) } 15 \qquad \textbf{(D) } 16 \qquad \textbf{(E) } 17$
$\textbf{A}$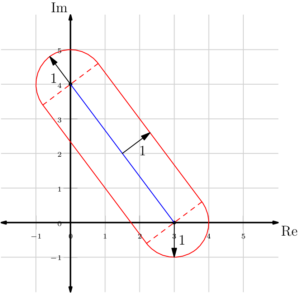
According to the given information, $z_1$ lies on the blue segment in the graph, and $z=z_1+z_2$ could be at most 1 away from the blue segment. Hence, $z$ is confined to the area within the red curve, which consists of a rectangle with a width of 2 and a length of 5, and a circle with radius 1. So the area of $\mathcal{R}$ is $5\times2 + \pi\times1^2=10+\pi \approx 10 + 3 = 13$.
What is the value of\[(\log 5)^3+(\log 20)^3+(\log 8)(\log 0.25)\]where $\log$ denotes the base-ten logarithm?
$\textbf{(A) } \dfrac{3}{2} \qquad \textbf{(B) } \dfrac{7}{4} \qquad \textbf{(C) } 2 \qquad \textbf{(D) } \dfrac{9}{4} \qquad \textbf{(E) } 3$
$\textbf{C}$
Let $\text{log } 2 = x$. Then we have \begin{align*}
\log 5&=\log 10-\log 2=1-x\\
\log 20&=\log 10+\log 2=1+x\\
\log 8&=\log 2^3=3\log 2=3x\\
\log 0.25&=\log 2^{-2}=-2\log 2=-2x
\end{align*} The original expression becomes\[(1-x)^3+(1+x)^3+(3x)(-2x)=2\]
The roots of the polynomial $10x^3 - 39x^2 + 29x - 6$ are the height, length, and width of a rectangular box (right rectangular prism). A new rectangular box is formed by lengthening each edge of the original box by $2$ units. What is the volume of the new box?
$\textbf{(A) } \dfrac{24}{5} \qquad \textbf{(B) } \dfrac{42}{5} \qquad \textbf{(C) } \dfrac{81}{5} \qquad \textbf{(D) } 30 \qquad \textbf{(E) } 48$
$\textbf{D}$
Let $a,b,c$ be the roots of the polynomial. By Vieta's formulas, we have \begin{align*}
a+b+c&=\dfrac{39}{10}\\
ab+ac+bc&=\dfrac{29}{10}\\
abc&=\dfrac{6}{10}
\end{align*} The volume of the new box is $$(a+2)(b+2)(c+2)=abc+2(ab+ac+bc)+4(a+b+c)+8=30$$
A triangular number is a positive integer that can be expressed in the form $t_n=1+2+3+\cdots+n$, for some positive integer $n$. The three smallest triangular numbers that are also perfect squares are $t_1=1=1^2, t_8=36=6^2,$ and $t_{49}=1225=35^2$. What is the sum of the digits of the fourth smallest triangular number that is also a perfect square?
$\textbf{(A)} ~6 \qquad\textbf{(B)} ~9 \qquad\textbf{(C)} ~12 \qquad\textbf{(D)} ~18 \qquad\textbf{(E)} ~27$
$\textbf{D}$
We see that $t_n=1+2+3+\cdots+n=\dfrac{n(n+1)}{2}$. If $t_n$ is a perfect square, then it can be written as $\dfrac{n (n+1)}{2} = k^2$, where $k$ is a positive integer. Thus, we have $$n(n+1)=2k^2$$ Since $n$ and $n+1$ are consecutive integers, they must be relatively prime. Assuming that the prime factorization of $k$ gives $k=p_1^{\alpha_1}\cdot p_2^{\alpha_2}\cdots p_i^{\alpha_i}$. In order to make $n$ and $n+1$ relatively prime, all the powers of each prime factor $p_i$ must all belong to either $n$ or $n+1$. Therefore, we have two cases:
$\textbf{Case 1}:$ $n$ is a perfect square. Since the right side of the equation is $2k^2$, in this case $n+1$ is twice a square number.
$\textbf{Case 2}:$ $n+1$ is a perfect square. Similarly, in this case $n$ is twice a square number.
We see that $n$ is either a square number or is 1 less than a square number. Thus, we try $n=63$ or $64$ first, which didn't work. Then we try $n=80,81,99,100,120,121\cdots$
Finally, we found that if $n=288=17^2-1$, $t_{288}=\dfrac{288\times289}{2}=144\times289=41616$ is a perfect square. So the answer is $4+1+6+1+6=18$.
Suppose $a$ is a real number such that the equation\[a\cdot(\sin{x}+\sin{(2x)}) = \sin{(3x)}\]has more than one solution in the interval $(0, \pi)$. The set of all such $a$ that can be written in the form\[(p,q) \cup (q,r),\]where $p, q,$ and $r$ are real numbers with $p < q< r$. What is $p+q+r$?
$\textbf{(A) } {-}4 \qquad \textbf{(B) } {-}1 \qquad \textbf{(C) } 0 \qquad \textbf{(D) } 1 \qquad \textbf{(E) } 4$
$\textbf{A}$
Noticing that $\sin(2x)=2\sin x\cos x$, and $\sin{(3x)} = \sin{x}\cdot(4\cos^2{x}-1)$. Substituting $\sin(2x)$ and $\sin(3x)$ into the original expression, we have \[a\cdot(\sin{x}+2\sin{x}\cos{x})=\sin{x}\cdot(4\cos^2{x}-1)\] Since $\sin{x} \ne 0$ as it is on the open interval $(0, \pi)$, we can divide out $\sin{x}$ from both sides, leaving us with\[a\cdot(1+2\cos{x})=4\cos^2{x}-1\] Obviously, $\cos x=-\dfrac12$ is a valid solution. This gives $x = \dfrac{2\pi}{3}$.
If $\cos x\ne -\dfrac12$, then we have \[a = \frac{4\cos^2{x}-1}{1+2\cos{x}} = 2\cos x - 1\] which gives \[\cos x = \frac{a+1}{2}\] As $x\in (0, \pi)$, $\cos{x}\in (-1, 1)$, and therefore $\dfrac{a+1}{2}\in (-1, 1)$, so $a\in(-3,1)$.
There is one more case we must consider inside this interval though, the case where $\dfrac{a+1}{2} = -\dfrac{1}{2}$, as this would lead to a double root for $\cos{x}$, yielding only one valid solution for $x$. Solving for this case, $a \ne -2$.
Therefore, combining this fact with our solution interval, $a\in(-3, -2) \cup (-2, 1)$, so the answer is $-3-2+1 = {-}4$.
Let $T_k$ be the transformation of the coordinate plane that first rotates the plane $k$ degrees counterclockwise around the origin and then reflects the plane across the $y$-axis. What is the least positive integer $n$ such that performing the sequence of transformations $T_1, T_2, T_3,...,T_n$ returns the point $(1, 0)$ back to itself?
$\textbf{(A) } 359 \qquad \textbf{(B) } 360 \qquad \textbf{(C) } 719 \qquad \textbf{(D) } 720 \qquad \textbf{(E) } 721$
$\textbf{A}$
Let $P=(r,\theta)$ be a point in polar coordinates, where $\theta$ is in degrees.
Rotating $P$ by $k^{\circ}$ counterclockwise around the origin gives the transformation $(r,\theta)\rightarrow(r,\theta+k^{\circ}).$ Reflecting $P$ across the $y$-axis gives the transformation $(r,\theta)\rightarrow(r,180^{\circ}-\theta).$ Note that\begin{align*} T_k(P)&=(r,180^{\circ}-\theta-k^{\circ}) \\ T_{k+1}(T_k(P)) &= (r,\theta -1^{\circ}) \end{align*}We start with $(1,0^{\circ})$ in polar coordinates. For the sequence of transformations $T_1, T_2, T_3, \cdots, T_k,$ it follows that
After $T_1,$ we have $(1,179^{\circ}).$$\newline$
After $T_2,$ we have $(1,-1^{\circ}).$$\newline$
After $T_3,$ we have $(1,178^{\circ}).$$\newline$
After $T_4,$ we have $(1,-2^{\circ}).$$\newline$
After $T_5,$ we have $(1,177^{\circ}).$$\newline$
After $T_6,$ we have $(1,-3^{\circ}).$$\newline$
$\cdots\newline$
After $T_{2k-1},$ we have $(1,180^{\circ}-k^{\circ}).$$\newline$
After $T_{2k},$ we have $(1,-k^{\circ}).$
The least such positive integer $k$ is $180.$ Therefore, the least such positive integer $n$ is $2k-1= 359.$
Suppose that $13$ cards numbered $1, 2, 3, \ldots, 13$ are arranged in a row. The task is to pick them up in numerically increasing order, working repeatedly from left to right. In the example below, cards $1, 2, 3$ are picked up on the first pass, $4$ and $5$ on the second pass, $6$ on the third pass, $7, 8, 9, 10$ on the fourth pass, and $11, 12, 13$ on the fifth pass. For how many of the $13!$ possible orderings of the cards will the $13$ cards be picked up in exactly two passes?![]()
$\textbf{(A) } 4082 \qquad \textbf{(B) } 4095 \qquad \textbf{(C) } 4096 \qquad \textbf{(D) } 8178 \qquad \textbf{(E) } 8191$
$\textbf{D}$
Since the $13$ cards are picked up in two passes, the first pass must pick up the first $n$ cards and the second pass must pick up the remaining cards $n+1$ through $13$. Also note that if $n+1$ is placed before $n$, then $n+1$ will not be picked up on the first pass since cards are picked up in order. Therefore, we want $n+1$ to be placed before $n$ to create a second pass, and that after the first pass, the numbers $n+1$ through $13$ are lined up in order from least to greatest.
To construct this, $n$ cannot be placed in the $n$th position because all cards $1$ to $n-1$ will have to precede it and there will be no room for $n+1$. Therefore, we have $\dbinom{13}{n}-1$ ways to arrange cards $1$ to $n$. Once the positions of the first $n$ cards are confirmed, there is only one way to arrange the rest cards.
Hence, the total number of arrangements is\[\sum_{n=1}^{12}\left[\binom{13}{n}-1\right] = \left[\sum_{n=1}^{12}\binom{13}{n}\right]-12 = \left[\sum_{n=0}^{13}\binom{13}{n}\right]-14 = 2^{13} - 14 = 8178\]
Isosceles trapezoid $ABCD$ has parallel sides $\overline{AD}$ and $\overline{BC},$ with $BC < AD$ and $AB = CD.$ There is a point $P$ in the plane such that $PA=1, PB=2, PC=3,$ and $PD=4.$ What is $\dfrac{BC}{AD}?$
$\textbf{(A) }\dfrac{1}{4}\qquad\textbf{(B) }\dfrac{1}{3}\qquad\textbf{(C) }\dfrac{1}{2}\qquad\textbf{(D) }\dfrac{2}{3}\qquad\textbf{(E) }\dfrac{3}{4}$
$\textbf{B}$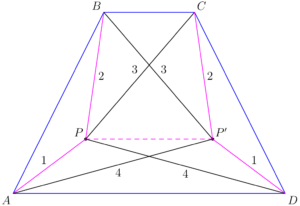
Consider the reflection $P^{\prime}$ of $P$ over the perpendicular bisector of $\overline{BC}$, creating two new isosceles trapezoids $DAPP^{\prime}$ and $CBPP^{\prime}$. Under this reflection, $P^{\prime}D=PA=1$, $P^{\prime}C=PB=2$, $P^{\prime}B=PC=3$, and $P^{\prime}A=PD=4$.
Since $DAPP'$ and $CBPP'$ are isosceles trapezoids, they are cyclic. Using Ptolemy's theorem on $DAPP'$, we get that $PP'\cdot AD + PA\cdot P'D= AP'\cdot PD$, so\[PP' \cdot AD + 1 \times 1 = 4 \times 4\]Then, using Ptolemy's theorem again on $CBPP'$, we get that $BC\cdot PP' + BP\cdot CP' = BP'\cdot CP$, so\[PP' \cdot BC + 2 \times 2 = 3 \times 3\]Thus, we get $PP^{\prime}\cdot AD=15$ and $PP^{\prime}\cdot BC=5$. Dividing these two equations yields $\dfrac{BC}{AD}= \dfrac{1}{3}$.
Let\[P(x) = x^{2022} + x^{1011} + 1.\]Which of the following polynomials is a factor of $P(x)$?
$\textbf{(A)} \, x^2 -x + 1 \qquad\textbf{(B)} \, x^2 + x + 1 \qquad\textbf{(C)} \, x^4 + 1 \qquad\textbf{(D)} \, x^6 - x^3 + 1 \qquad\textbf{(E)} \, x^6 + x^3 + 1$
$\textbf{E}$
\[P(x)=x^{2022}+x^{1011}+1=\frac{x^{3033}-1}{x^{1011}-1}\] The roots of $x^{3033}-1$ are in the form of $x=e^{i\cdot\frac{2k\pi}{3033}}$, where $1\leq k\leq 3033$ is an integer. Similarly, the roots of $x^{1011}-1$ are in the form of $x=e^{i\cdot\frac{2k\pi}{1011}}$, where $1\leq k\leq 1011$ is an integer. Hence, the roots of $P(x) = x^{2022} + x^{1011} + 1$ are in the form of $x=e^{i\cdot\frac{2k\pi}{3033}}$, where $1\leq k\leq 3033$ is an integer but not a multiple of 3.
Note that a monic polynomial $q$ divides a monic polynomial $p$ if and only if all the roots of $q$ are roots of $p.$ Hence, all the roots of a polynomial factor of $P(x) = x^{2022} + x^{1011} + 1$ must be roots of $x^{3033}-1$ but not $x^{1011}-1$.
We know that any polynomial $x^m-1$ divides $x^n-1$ if and only if $m$ is a factor of $n$. The prime factorizations of $1011$ and $3033$ are $3\times337$ and $3^2\times337$, respectively. Hence, $x^9-1$ is a divisor of $x^{3033}-1$ but not $x^{1011}-1$. However, some roots of $x^9-1$ are also roots of $x^{1011}-1$, and they should be excluded.
The roots of $x^9-1$ are $x=e^{i\cdot\frac{2k\pi}{9}}=e^{i\cdot\frac{2\cdot 337k\pi}{3033}}$, where $1\leq k\leq 9$ is an integer. When $k=3,6,9$, $x=e^{i\cdot\frac{2k\pi}{9}}$ are roots of $x^{1011}-1$. To exclude these roots, we have $x^9-1=(x^3-1)(x^6+x^3+1)$. Now all roots of $x^6+x^3+1$ are roots of $x^{3033}-1$ but not $x^{1011}-1$.
Therefore, the answer is E.
Let $c$ be a real number, and let $z_1$ and $z_2$ be the two complex numbers satisfying the equation $z^2 - cz + 10 = 0$. Points $z_1$, $z_2$, $\dfrac{1}{z_1}$, and $\dfrac{1}{z_2}$ are the vertices of (convex) quadrilateral $\mathcal{Q}$ in the complex plane. When the area of $\mathcal{Q}$ obtains its maximum possible value, $c$ is closest to which of the following?
$\textbf{(A) }4.5 \qquad\textbf{(B) }5 \qquad\textbf{(C) }5.5 \qquad\textbf{(D) }6\qquad\textbf{(E) }6.5$
$\textbf{A}$
By Vieta's formula, we have \begin{align*}
z_1+z_2&=c\\
z_1z_2&=10
\end{align*} Since $c$ is a real number, we have $z_2 = \bar z_1$. Then we get $$z_1+z_2=z_1+\bar z_1=2 {\rm Re}(z_1)=c$$ $$z_1z_2=z_1\bar z_1=|z_1|^2=10$$ $$ \frac{1}{z_1} = \frac{1}{10}\cdot\frac{10}{z_1} = \frac{1}{10}\cdot\frac{z_1 z_2}{z_1} = \frac{z_2}{10} = \frac{\bar z_1}{10}$$ $$ \frac{1}{z_2} = \frac{1}{10}\cdot\frac{10}{z_2} = \frac{1}{10}\cdot\frac{z_1 z_2}{z_2} = \frac{z_1}{10}$$ The figure of the quadrilateral $\mathcal{Q}$ in the complex plane is shown below: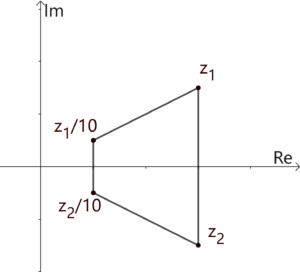
We see that quadrilateral $\mathcal{Q}$ is an isosceles trapezoid. So its area is \begin{align*}
\dfrac12\left[2{\rm Im}(z_1)+2\cdot\dfrac1{10}{\rm Im}(z_1)\right]\cdot\left[{\rm Re}(z_1)-\dfrac1{10}{\rm Re}(z_1)\right]&=\dfrac{99}{100}{\rm Re}(z_1){\rm Im}(z_1)\\
&\leq\dfrac{99}{100}\cdot\dfrac{{\rm Re}^2(z_1)+{\rm Im}^2(z_1)}{2}\\
&=\dfrac{99}{100}\cdot\dfrac{|z_1|^2}{2}\\
&=\dfrac{99}{100}\cdot\dfrac{10}{2}\\
&=\dfrac{99}{20}
\end{align*} The area of $\mathcal{Q}$ reaches its maximum value when ${\rm Re}(z_1)={\rm Im}(z_1)$. We know that ${\rm Re}(z_1)=\dfrac{c}2$, so $$|z_1|^2={\rm Re}^2(z_1)+{\rm Im}^2(z_1)=\left(\dfrac{c}2\right)^2+\left(\dfrac{c}2\right)^2=10\rightarrow c=2\sqrt5\approx4.5$$
Let $h_n$ and $k_n$ be the unique relatively prime positive integers such that\[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}=\frac{h_n}{k_n}.\]Let $L_n$ denote the least common multiple of the numbers $1, 2, 3, \ldots, n$. For how many integers with $1\le{n}\le{22}$ is $k_n<L_n$?
$\textbf{(A) }0 \qquad\textbf{(B) }3 \qquad\textbf{(C) }7 \qquad\textbf{(D) }8\qquad\textbf{(E) }10$
$\textbf{D}$
Note that $$\sum_{i=1}^{n}\frac{1}{i} = \frac{\sum_{i=1}^{n}\frac{L_n}{i}}{L_n}=\dfrac{h_n}{k_n}$$ Thus, in order for $L_n$ to reduce to a smaller value ($k_n<L_n$), the numerator and denominator must share a common factor.
Let the prime factorization of $L_n$ be $L_n=p_1^{\alpha_1}\cdot p_2^{\alpha_2}\cdots p_j^{\alpha_j}$, where each term must be no more than $n$ as $p^{\alpha}\leq n$. It is clear that for each prime $p$, $L_n\equiv0\pmod{p},$ so we need to test whether $$\sum_{i=1}^{n}\frac{L_n}{i}\equiv0\pmod{p}$$ If $i$ is a multiple of $p^\beta$ where $\beta<\alpha$, then we can be certain that $\dfrac{L_n}{i}\equiv0\pmod{p}$. However, for those $i$ who is a multiple of $p^\alpha$, although each of them do not satisfy $\dfrac{L_n}{i}\equiv0\pmod{p}$, the sum of them might work, as \[\sum_{i=1}^{\left\lfloor\tfrac{n}{p^\alpha}\right\rfloor}\frac{L_n}{ip^\alpha} \equiv 0\pmod{p}\] Actually, we don't need to calculate each $L_n$. We just need to find \[\sum_{i=1}^{\left\lfloor\tfrac{n}{p^\alpha}\right\rfloor}\frac{1}{i}=\dfrac{u}{v}\] where $u$ and $v$ are relatively prime. We have $k_n < L_n$ if and only if $u$ is a multiple of $p$.
All the primes $p$ under 22 are 2,3,5,7,11,13,17,19. First, we can prove that $\sum_{i=1}^{n}\dfrac{L_n}{i}\equiv0\pmod{p}$ doesn't work for $p=2$. Let $2^\alpha$ be the largest power of 2 such that $2^\alpha$ divides $L_n$. Notice that among all numbers $1$ through $n$, only one of them can be a multiple of $2^\alpha$, being $2^\alpha$ itself. The next multiple of $2^\alpha$ would be $2 \cdot 2^\alpha = 2^{\alpha+1}$, contradicting the fact that $2^\alpha$ is the largest power of 2 such that $2^\alpha$ divides $L_n$. This means that in the sum $\sum_{i=1}^{n}\dfrac{L_n}{i}$, there will be only $1$ value that is $1$ mod $2$, resulting from $\dfrac{L_n}{2^\alpha}$, and the rest are all $0$s. Clearly, the sum $\sum_{i=1}^{n}\dfrac{L_n}{i}$ will then be $1$ mod $2$, which is not a multiple of 2.
We have another way to prove $p=2$ doesn't work. Recall $\sum_{i=1}^{\left\lfloor\tfrac{n}{p^\alpha}\right\rfloor}\dfrac{1}{i}=\dfrac{u}{v}$. Apparently $\left\lfloor\dfrac{n}{2^\alpha}\right\rfloor=1$ because $2^\alpha\leq n<2^{\alpha+1}$. So $\sum_{i=1}^{\left\lfloor\tfrac{n}{2^\alpha}\right\rfloor}\dfrac{1}{i}=\sum_{i=1}^1\dfrac1i=\dfrac11$, where the numerator 1 is not a multiple of 2. So $p=2$ leads to $k_n=L_n$.
Next, when $p=3$, we can find out that $n=6,7,8,18,19,20,21,22$ work. For example, if $n=6,7,8$, the highest power of prime 3 is $\alpha=1$. Then we have $\left\lfloor\dfrac{n}{3^1}\right\rfloor=2$, $\sum_{i=1}^{\left\lfloor\tfrac{n}{p^\alpha}\right\rfloor}\dfrac{1}{i}=\sum_{i=1}^{2}\dfrac{1}{i}=\dfrac32$, where the numerator 3 is a multiple of prime 3. If $n=18,19,20,21,22$, the highest power of prime 3 is $\alpha=2$. Then we have $\left\lfloor\dfrac{n}{3^2}\right\rfloor=2$, $\sum_{i=1}^{\left\lfloor\tfrac{n}{p^\alpha}\right\rfloor}\dfrac{1}{i}=\sum_{i=1}^{2}\dfrac{1}{i}=\dfrac32$, where the numerator 3 is again a multiple of prime 3.
When $p=5$, its highest power is 1 for $n\leq22$. Since the numerators of $\sum_i^1\dfrac1i=\dfrac11$, $\sum_i^2\dfrac1i=\dfrac32$ and $\sum_i^3\dfrac1i=\dfrac{11}6$ are not multiples of 5, but $\sum_i^4\dfrac1i=\dfrac{25}{12}$ satisfies the condition, we find out that $n\geq5^1\cdot4=20$ works, namely $n=20,21,22$.
When $p=7$, $\left\lfloor\dfrac{n}{p^\alpha}\right\rfloor$ can be 1, 2 or 3. However, none of the numerators of $\sum_i^1\dfrac1i=\dfrac11$, $\sum_i^2\dfrac1i=\dfrac32$ and $\sum_i^3\dfrac1i=\dfrac{11}6$ can be a multiple of 7. So $p=7$ doesn't work.
When $p=11$, $\left\lfloor\dfrac{n}{p^\alpha}\right\rfloor$ can be 1 or 2. Now the numerators of $\sum_i^1\dfrac1i=\dfrac11$ and $\sum_i^2\dfrac1i=\dfrac32$ are not multiples of 11. So $p=11$ doesn't work.
When $p=13,17,19$, $\left\lfloor\dfrac{n}{p^\alpha}\right\rfloor$ can only be 1. Again the numerator of $\sum_i^1\dfrac1i=\dfrac11$ is not a multiple of 13, 17 or 19. So $p=13,17,19$ don't work.
In conclusion, we have $n=6,7,8,18,19,20,21,22$ which can lead to $\sum_{i=1}^{n}\dfrac{L_n}{i}\equiv0\pmod{p}$, and furthermore, $k_n<L_n$. So the total number of integers that satisfies $k_n<L_n$ is 8.
How many strings of length $5$ formed from the digits $0$, $1$, $2$, $3$, $4$ are there such that for each $j \in \{1,2,3,4\}$, at least $j$ of the digits are less than $j$? (For example, $02214$ satisfies this condition because it contains at least $1$ digit less than $1$, at least $2$ digits less than $2$, at least $3$ digits less than $3$, and at least $4$ digits less than $4$. The string $23404$ does not satisfy the condition because it does not contain at least $2$ digits less than $2$.)
$\textbf{(A) }500\qquad\textbf{(B) }625\qquad\textbf{(C) }1089\qquad\textbf{(D) }1199\qquad\textbf{(E) }1296$
$\textbf{E}$
Let's call the condition where you require at least $j$ digits less than $j$ Rule $j$.
For a sequence to break Rule $1$, it must contain no $0$s. There are $4^5=1024$ ways to do this.
For a sequence to break Rule $2$ but not Rule $1$, it must contain exactly one $0$, and all other digits must be no less than $2$. After placing the one $0$ in any of $5$ slots, there are $4$ slots left with $3$ options each, giving a total of $5 \times 3^4 = 405$ ways.
For a sequence to break Rule $3$ but neither Rule $2$ or $1$, it must have two digits less than $2$ (either $(0, 0)$ or $(0, 1)$) and all other digits must be $3$ or $4$. There are a total of $\dbinom52+5\times4=30$ ways to arrange the first two digits, and $2^3$ ways to arrange the other three, leaving $30\times2^3=240$ ways to do this.
Finally, for a sequence to only break Rule $4$, it must have three digits less than $3$. They could be $(0, 1, 2)$ with $5\times4\times3=60$ arrangements, or $(0, 1, 1)(0, 0, 1)(0, 0, 2)$ with $5\times\dbinom42=30$ arrangements each, or $(0, 0, 0)$ with $\dbinom53=10$ arrangements. This gives $60+30\times3+10=160$ possible arrangements overall. The remaining two digits must be two 4s.
There are in total $5^5=3125$ possible arrangements, so by adding all of the invalid states together and subtracting from $3125$, we get our answer $3125-(1024+405+240+160)=1296$.
A circle with integer radius $r$ is centered at $(r, r)$. Distinct line segments of length $c_i$ connect points $(0, a_i)$ to $(b_i, 0)$ for $1 \le i \le 14$ and are tangent to the circle, where $a_i$, $b_i$, and $c_i$ are all positive integers and $c_1 \le c_2 \le \cdots \le c_{14}$. What is the ratio $\dfrac{c_{14}}{c_1}$ for the least possible value of $r$?
$\textbf{(A)} ~\dfrac{21}{5} \qquad\textbf{(B)} ~\dfrac{85}{13} \qquad\textbf{(C)} ~7 \qquad\textbf{(D)} ~\dfrac{39}{5} \qquad\textbf{(E)} ~17$
$\textbf{E}$
Since the origin and the circle may lie on the same side or the opposite sides of the tangent, we have 2 cases.
$\textbf{Case 1}$: The origin and the circle lie on the same side of the tangent.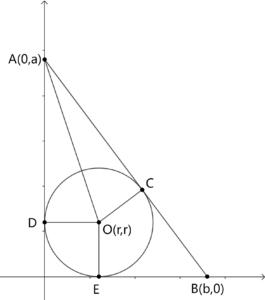
In this case we have $a,b>2r$. Since $OC\perp AB$, $OD\perp AD$, $OE\perp BE$, we have $AC=AD=a-r$, $BC=BE=b-r$. So the length of the hypotenuse is $c=(a-r)+(b-r)=a+b-2r$.
$\textbf{Case 2}$: The origin and the circle lie on the opposite sides of the tangent.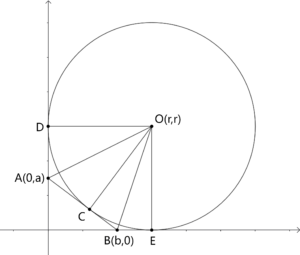
In this case we have $a,b<r$. Since $OC\perp AB$, $OD\perp AD$, $OE\perp BE$, we have $AC=AD=r-a$, $BC=BE=r-b$. So the length of the hypotenuse is $c=(r-a)+(r-b)=2r-a-b$.
By the Pythagorean theorem, $c^2=a^2+b^2$. No matter in which case, we have $a^2+b^2=(a+b-2r)^2$, which can be simplified as \[\left( a - 2 r \right) \left( b - 2 r \right) = 2 r^2 \] with either $a, b > 2r$ or $0 < a, b < r$.
Now we need to find the smallest $r$, such that the number of feasible solutions of $(a, b)$ is at least 14.
For equation\[uv = 2 r^2 ,\]we observe that the right side of the equation is a not a perfect square. Thus, the number of positive $(u, v)$ is equal to the number of positive divisors of $2 r^2$. (We can switch the order of $(u, v)$ as $(v, u)$.)
Second, for each feasible positive solution $(u, v)$, its opposite $(-u, -v)$ is also a solution. However, each $(u,v)$ corresponds to a feasible solution with $a = u + 2r$ and $b = v + 2r$, but each $(-u, -v)$ may not lead to a feasible solution with $a = 2 r - u$ and $b = 2 r - v$ because $u$ or $v$ may be no less than $2r$.
Recall that we are looking for $r$ that leads to at least 14 solutions. Therefore, the above observations imply that we must have $r$, such that $2 r^2$ has least 7 positive divisors.
Following this guidance, we find that:$\newline$
$r=1$ doesn't work because $2r^2=2^1$ has only $1+1=2$ positive divisors. $\newline$
$r=2$ doesn't work because $2r^2=2^3$ has only $3+1=4$ positive divisors.$\newline$
$r=3$ doesn't work because $2r^2=2^1\cdot3^2$ has only $(1+1)(2+1)=6$ positive divisors.$\newline$
$r=4$ doesn't work because $2r^2=2^5$ has only $5+1=6$ positive divisors. $\newline$
$r=5$ doesn't work because $2r^2=2^1\cdot5^2$ has only $(1+1)(2+1)=6$ positive divisors.
Then we try $r=6$. $2r^2=2^3\cdot3^2$ has 12 positives divisors, which gives 12 positive $(u,v)$ pairs. Now we want to find at least 2 $(-u,-v)$ pairs to make a total of 14 solutions. Fortunately, we find out that $(-u,-v)=(-8,-9)$ and $(-9,-8)$ work. So the smallest value of $r$ is 6.
When $r=6$, $c$ reaches its smallest possible value when the origin and the circle lie on the opposite sides of the tangent, as Case 2. Now we have $c=2r-a-b=12-a-b$. The minimum value occurs at $(-u,-v)=(-8,-9)$ (or vice versa), where $(a,b)=(2r-u,2r-v)=(4,3)$. So the minimum value of $c$ is $c_1=5$.
$c$ reaches its largest possible value when the origin and the circle lie on the same side of the tangent, as Case 1. Now we have $c=a+b-2r=a+b-12$. The maximum value occurs at $(u,v)=(72,1)$, where $(a,b)=(u+2r,v+2r)=(84,13)$. So the maximum value of $c$ is $c_{14}=a+b-12=85$.
Hence, the answer is $\dfrac{c_{14}}{c_1}=\dfrac{85}5=17$.